| 1.1.1 The Real Numbers : |
Real Numbers are the elements of a set, denoted by 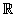 , with the following properties: , with the following properties: |
| 1) Algebraic properties of real numbers: |
| |
There are two binary operations defined on 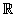 , one called addition, denoted by , one called addition, denoted by
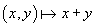 , and the other called multiplication, denoted by , and the other called multiplication, denoted by
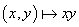 , with the usual algebric properties: for all , with the usual algebric properties: for all
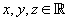 |
 |
 . . |
 |
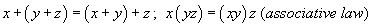 . . |
 |
 . . |
| |
There exist two distinct elements in 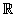 , denoted by 0 and 1, with following properties: , denoted by 0 and 1, with following properties: |
| |
0 + 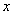 = = 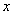 for all for all 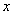  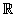 ; 1 ; 1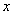 = = 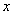 for all 0 for all 0 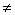 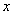  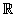 . .
The elements 0, read as zero, is called the additive identity and 1, read as one, is called the multiplicative identity. |

|
For every 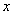  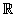 , there exists unique element , there exists unique element   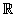 such that such that 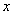 + (- + (-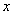 ) = 0 ; for ) = 0 ; for 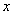 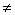 0 in 0 in 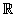 , there exists unique element , there exists unique element   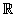 such that such that 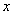 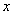  = 1. = 1. |
| |
| 2) Order properties of real numbers: |
There exists an order, denoted by <, between the elements of  with the following properties: with the following properties: |
 |
For 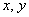   , one and only one of the following relations hold : , one and only one of the following relations hold : 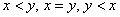 . . |
 |
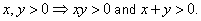 |
 |
 . . |
| |
There are two more properties that real numbers have which we shall describe later : |
| |
|
| 3) |
Archimedean property |