| |
A function f is called an algebraic function if it can be obtained from integral polynomial functions in finite number of operations involving one or more of the following operations:
sums / products / quotients / taking inverse. Functions which are not algebraic are called transcendental functions.
|
| |
The most important among the transcendental functions are the natural logarithmic function and its inverse, the exponential function, and the trigonometric functions. We shall define these functions rigorously in module 6. For the time being, to illustrate various concepts, we shall assume the knowledge about trigonometric functions.
In particular we shall assume the following inequalities: For 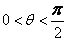 . .
- 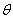 < sin < sin 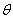 < < 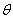 , - , - 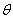 < 1 - cos < 1 - cos 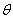 < < 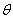 , , 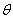 cos cos 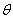 < sin < sin 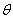 < < 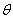
. |