| |
| 1.1.8 |
Note: Why real numbers? |
| |
At this stage one can ask the following questions: What is the need to work with real numbers? Can one not work always with rational numbers? How real numbers are different from rational numbers? You will see answer to some of these questions in this course. Hopefully, you would have realized by now that arithmetic is necessary for day-to-day life. |
| |
Also, you would have seen (in your school courses) that there does not exist any rational r such that 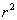 = 2. (This was discovered by the Greek mathematicians in 500 B.C.) This is one of the reasons why mathematicians were forced to invent a set of numbers which is 'bigger' than that of rationals, and which satisfy equations of the type = 2. (This was discovered by the Greek mathematicians in 500 B.C.) This is one of the reasons why mathematicians were forced to invent a set of numbers which is 'bigger' than that of rationals, and which satisfy equations of the type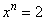 for all for all 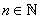 . The property of the real numbers that distinguishes them from the rational numbers, is called the completeness property, which we shall discuss in section 1.6 of lecture 3. Geometrically, rational numbers when represented by points on the line, do not cover every point of the line. For example, the point Q on the line such that OQ is equal to OA, the length of the diagonal of a square with unit length, does not correspond to any rational number. . The property of the real numbers that distinguishes them from the rational numbers, is called the completeness property, which we shall discuss in section 1.6 of lecture 3. Geometrically, rational numbers when represented by points on the line, do not cover every point of the line. For example, the point Q on the line such that OQ is equal to OA, the length of the diagonal of a square with unit length, does not correspond to any rational number. |
| |
|
| |
Thus, some gaps are left when rational numbers are represented as points on a horizontal line. Filling up these gaps is the "completeness property" of the real numbers. We will make it mathematically precise in the next section. These gaps are the irrational numbers. |
| 1.1.9 |
Intervals : |
| |
We describe next another important class of subsets of  , called intervals. For a, b , called intervals. For a, b   with with 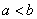 , we write , we write |
|
( a, b ) : = { x   | a < x < b }, [ a , b ] : = { x | a < x < b }, [ a , b ] : = { x   | a | a 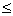 x x 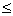 b }, b }, |
| |
( a, b ] : = { x   | a < x | a < x 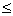 b }, [ a, b ) : = { x b }, [ a, b ) : = { x   | a | a 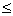 x < b }, x < b }, |
|
( a, + 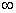 ) : = { x ) : = { x   | a < x }, [ a, + | a < x }, [ a, + 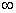 ) : = { x ) : = { x   | a | a 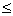 x }, x }, |
| |
( - 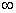 , a ] : = { x , a ] : = { x   | a | a 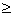 x }, ( - x }, ( -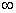 , a ) : = { x , a ) : = { x   | a > x }, | a > x }, |
|
|