| |
You already have some familiarity with the concept of a function. Function is a kind relation between various objects. For example, the volume 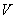 of a cube is a function of its side of a cube is a function of its side  ; in physics velocity ; in physics velocity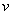 of a body at any time of a body at any time 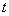 is a function of its initial velocity and time, and acceleration; and so on. In mathematics, a function is defined as follows: is a function of its initial velocity and time, and acceleration; and so on. In mathematics, a function is defined as follows:
|
(i)
|
For sets 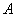 and and  , a function from , a function from 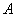 to to  , denoted by , denoted by  , is a correspondence which assigns to every element , is a correspondence which assigns to every element   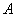 , a unique element , a unique element 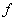 ( (  ) )   . The value of the function . The value of the function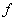 at an element at an element  in in 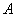 is denoted by is denoted by 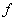 ( (  ), which is an element in ), which is an element in  . This is indicated by . This is indicated by 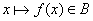 . . |
(ii)
|
For a function  , the set , the set 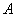 is called the domain of is called the domain of 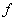 and the subset and the subset 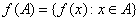 of of  , (set of images of , (set of images of 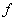 ) is called the range of ) is called the range of 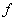 . If . If 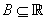 , then , then 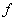 is said to be real-valued. If also is said to be real-valued. If also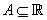 , then the natural domain of , then the natural domain of 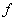 is the set of all is the set of all 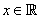 for which for which 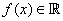 . . |
(i)
|
Let . Then, . Then, 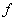 has natural domain has natural domain  . Its range is also . Its range is also  , because for any given , because for any given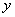 , ,
if  then we get then we get 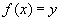 . . |
(ii) |
Let  . Then, . Then, 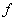 has natural domain has natural domain 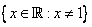 , and its range is given by , and its range is given by 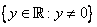 . . |
(iii) |
Let 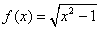 .Then, .Then, 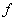 has natural domain has natural domain 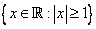 , and its range is given by , and its range is given by 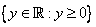 . . |
(i)
|
A real-valued function 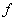 is said to be bounded if its range is a bounded subset of is said to be bounded if its range is a bounded subset of  , that is, there is some , that is, there is some
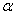   such that | such that | 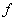 ( ( ) | ) | 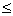 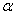 for all for all   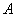 . . |
(ii)
|
Let 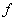 : : 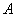 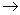  . The graph of . The graph of 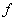 is the set : is the set :
G ( 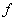 ) = { ( ) = { (  , , 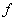 ( (  ) ) : ) ) :    } } 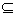  x x  . . |
(iii)
|
Let 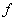 : : 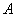 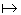 B be a function. We say B be a function. We say 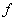 is one-one (or injective) if is one-one (or injective) if
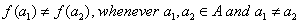 . . |