| |
Practice Exercises : Functions |
(1)
|
Let  be any set. For a subset be any set. For a subset 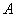 of of  , the indicator function of , the indicator function of 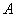 , denoted by , denoted by 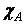 , is the function , is the function
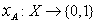 defined by defined by
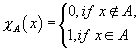 . . |
| |
Prove the following statements for 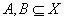 : : |
| |
Show that 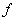 is a one-one function. Is it onto also? is a one-one function. Is it onto also?
( This shows that the set 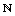 x x 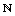 has as many points as has as many points as 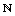 has ! ) has ! ) |
(3)
|
Let 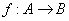 . For any set . For any set 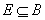 , let , let 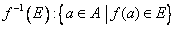 . .
The set  is called the preimage of is called the preimage of  . .
Prove the following: For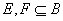 , , |
(e) |
If 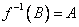 , then , then  need not be onto. need not be onto. |