| |
When a = b, interval ( a, a ) : = 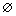 and [ a, a ] : = { a }. Intervals of the type (a ,b ] are called left-open right-closed intervals. and [ a, a ] : = { a }. Intervals of the type (a ,b ] are called left-open right-closed intervals. |
| |
Simililarly, intervals of the type [ a, b ) are called left-closed right-open Intervals. And intervals of the type ( a, b ), ( -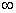 , a ), ( a, + , a ), ( a, +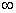 ) are called open intervals and of the type [ a,b ], ( - ) are called open intervals and of the type [ a,b ], ( -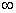 ,a ], ( a, + ,a ], ( a, +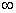 } are called closed intervals. Note that - } are called closed intervals. Note that -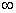 , + , +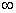 are just symbols, and not numbers. are just symbols, and not numbers.
|
| |
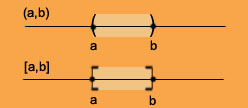
As stated above, shall assume that the set of real numbers can be identified with points on the straight line.
If point O represent the number 0, then points on the left of O represent negative real numbers and points on the right of O represent positive real numbers. Intervals are part of the line as shown: |
|
| |
This identification is useful in visualizing various properties of real numbers. An open interval of the type
(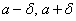 ) is called an ) is called an 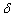 - neighborhood of a - neighborhood of a   . . |
|
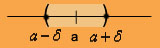  |
|