| |
| 4) |
Completeness property |
| |
Geometrically, set of all points on a line represent the set of all real numbers. There are some special subsets of  which are important. These are the familiar number systems. which are important. These are the familiar number systems. |
| 1.1.2 |
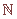 , the set of Natural Numbers: , the set of Natural Numbers: |
|
Recall that, there exist unique elements 0, 1   such that such that  , for x , for x   and and , for all 0 , for all 0 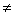 x x   .One can show that .One can show that . The set . The set 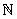 is the 'smallest' subset of is the 'smallest' subset of  having the property : having the property :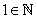 and and 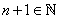 , whenever n , whenever n  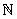 . This is also called the Principle of Mathematical Induction. One can show that such a subset of . This is also called the Principle of Mathematical Induction. One can show that such a subset of  exists, and is unique. Elements of exists, and is unique. Elements of 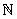 are called natural numbers. We shall use the familiar notation, are called natural numbers. We shall use the familiar notation, 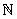 = {1,2,....,}. Geometrically, we can select any arbitrary point O on the real line and associate it with 0 = {1,2,....,}. Geometrically, we can select any arbitrary point O on the real line and associate it with 0   . Equidistant points on the right of O can be labeled as . Equidistant points on the right of O can be labeled as  |
 |
The set 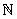 has the following properties, which we shall assume: has the following properties, which we shall assume:
|
 |
 for all for all 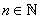 . . |
 |
For every  . . |
 |
For every 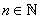 , there is no element m , there is no element m 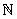 such that such that 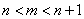 . . |
| |
|
 |
Archimedean property |
| |
For every 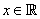 , there exists , there exists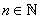 such that such that . . |
| |
|
| 1.1.3 |
Definition: |
(i)
|
A subset 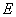 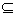  is said to be bounded above if there exists is said to be bounded above if there exists 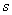   such that r such that r 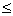 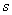 for all r for all r  E. That is, all the elements of E lie to the left of s, up to s at most. E. That is, all the elements of E lie to the left of s, up to s at most. |
| |
 |
|
|