|
For every 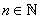 , let , let 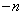 be the unique element of be the unique element of  such that such that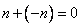 . Let . Let
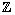 : = { ..., -2, -1, 0, 1, 2, ... } : = { ..., -2, -1, 0, 1, 2, ... }
Elements of 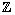 are called integers. Clearly, are called integers. Clearly, 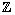 is neither bounded above nor bounded below. is neither bounded above nor bounded below. |
| |
For every 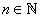 , let , let 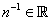 be such that be such that 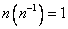 . The element . The element  is also denoted by is also denoted by 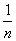 . Let . Let
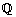 : = : = 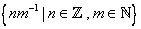
The set 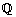 is called the set of rational numbers and the elements of the set is called the set of rational numbers and the elements of the set  \ \ 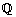 are called the irrational numbers. are called the irrational numbers.
Both, the rational and the irrational numbers have the following denseness property : |