(ii) For second natural frequency : State vectors are given as
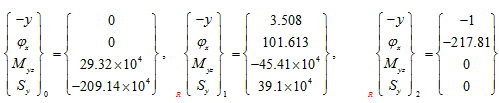
So that we have
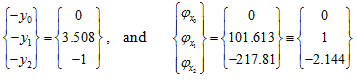
Figure 8.29 shows mode shape for y and φz corresponding to the second natural frequency.
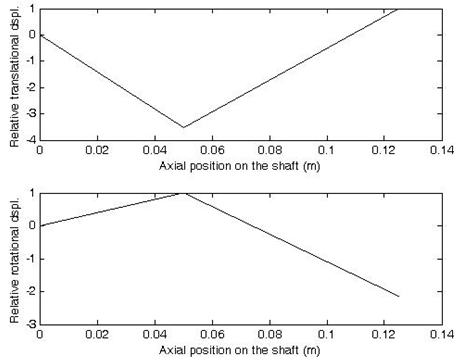
Fig. 8.29 Mode shapes corresponding to the second natural frequency (top) for the translational displacement and (bottom) for the rotational displacement
(iii) For third natural frequency: State vectors are given as
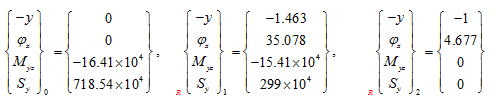
So that from above state vectors, we have
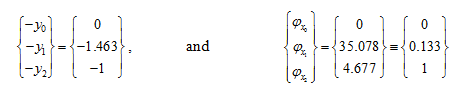
Figure 8.30 shows mode shape for y and φz corresponding to the third natural frequency.
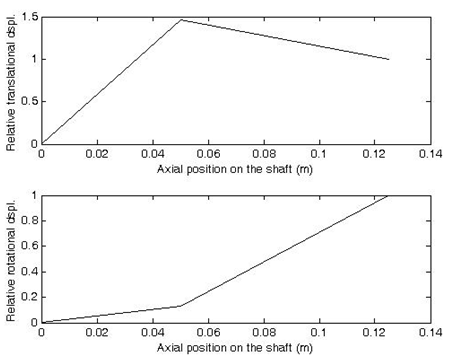
Fig. 8.30 Mode shapes corresponding to the third natural frequency (top) for the translational displacement and (bottom) for the rotational displacement
(iv) For fourth natural frequency: State vectors are given as
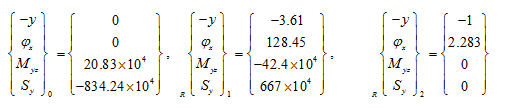
So that from above state vectors, we have
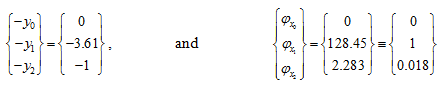
Figure 8.31 shows mode shape for y and φz corresponding to the fourth natural frequency.
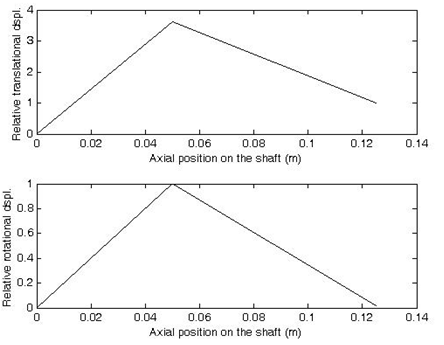
Fig. 8.31 Mode shapes corresponding to the fourth natural frequency (top) for the translational displacement and (bottom) for the rotational displacement