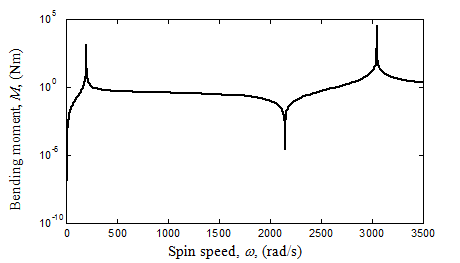
Figure 8.24(c) Variation of the support bending moment with the spin speed
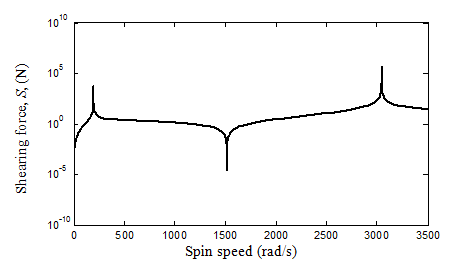
Figure 8.24(d) Variation of the support shearing force with the spin speed
Example 8.5 Obtain transverse natural frequencies and corresponding mode shapes of a rotor system as shown in Figure 8.25. Take the mass of the disc, m = 10 kg, the diametral mass moment of inertia, Id = 0.02 kg-m2 and the disc is placed at 0.25 m from the right support. The shaft has the diameter of 10 mm and the span length of 1 m. The shaft material has the Young's modulus E = 2.1 × 1011 N/m2 and consider the shaft as mass-less. Neglect gyroscopic effects and take one plane motion only. Compare the results by the influence coefficient method.
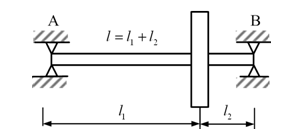
Figure 8.25 A simply supported rotor system
Solution : Station numbers 0, 1 and 2 can be assigned at the left support, at the disc and at the right support; respectively. Then, the overall transformation of states is given as
(a) |
which can be expanded as
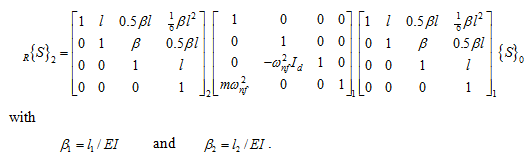 |
(b) |
Subscripts 1 and 2 outside the matrices belong to the following parameters: β, l, and Id. On multiplication of matrices, we get
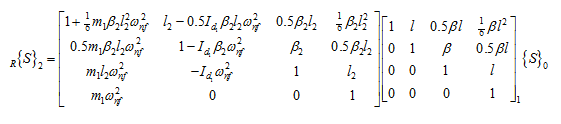
which finally takes the following form
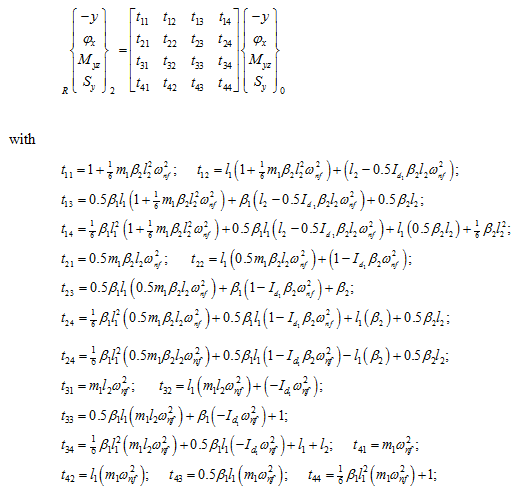 |
(c)
(d) |