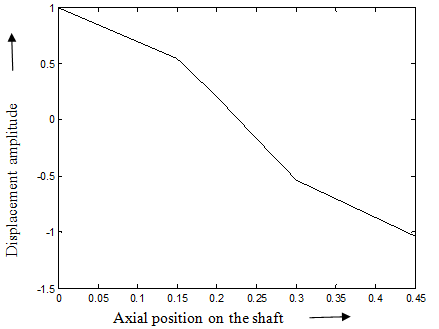
Fig. 8.33(b) The fundamental mode shape of rotational (slope) displacements

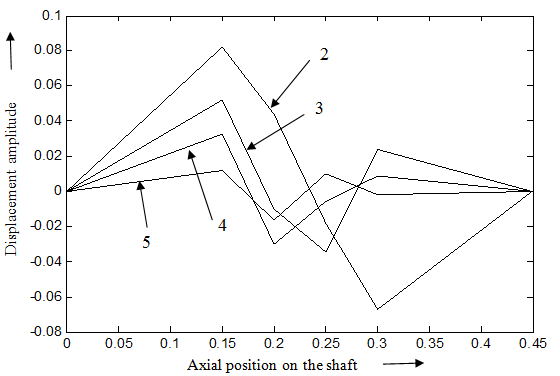
Fig. 8.33(c) Higher mode shapes (2^nd to 5^th) of translational displacements

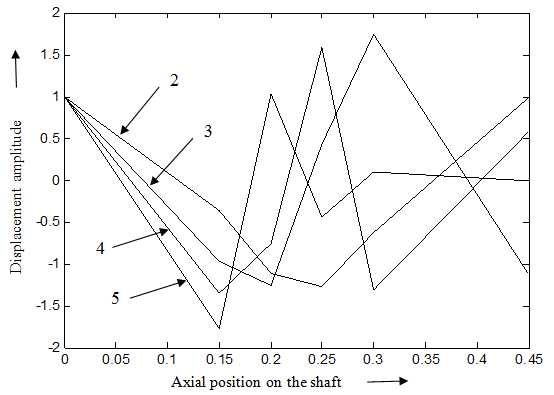
Fig. 8.33(d) Higher mode shapes (2^nd to 5^th) of rotational (slope) displacements

Answer .

Example 8.8 Obtain bending critical speeds of a rotor system as shown in Figure 8.34. Take the mass of the disc, m = 5 kg and its diametral mass moment of inertia, I_d = 0.02 kg-m² . The length of the shaft segments are a = 0.3 m and b = 0.7 m; and the diameter of the shaft is 0.01 m. Neglect the gyroscopic effects. E = 2.1 × 10¹¹ N/m² .

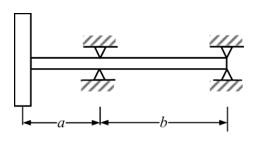
Figure 8.34 An overhang rotor system

Solution : Figure 8.35 shows the station numbering and free body diagram of various segments and supports.

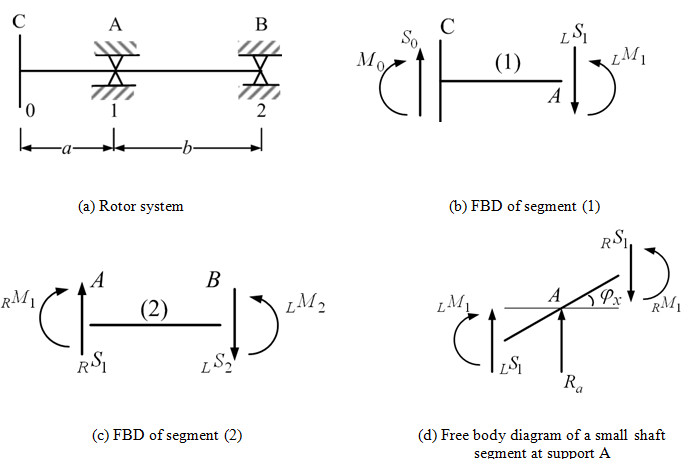
Figure 8.35 Free body diagrams of rotor segments