Exercise Problems

Use both the influence coefficient and transfer matrix methods for the entire problem unless otherwise stated in the problem. The Durkerley's formula could be used to rough estimate of the fundamental natural frequency.

Exercise 8.1 Obtain the transverse natural frequencies of a rotor as shown in Figure E8.1. The rotor is assumed to be fixed supported at one end and free at the other. Take mass of the disc m = 2 kg and its diametral mass moment of inertia I_d = 0.05 kg-m² . The shaft is assumed to be massless, and its length and diameter are 0.2 m and 0.01 m, respectively. Take the Young's modulus E = 2.1 × (10)¹¹ N/m² for the shaft material.

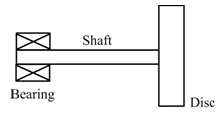
Figure E8.1

Exercise 8.2 Find the transverse natural frequencies and mode shapes of the rotor system shown in Figure E8.2 by the influence coefficient method. Take EI = 2 MNm² for the shaft and the diametral mass moment of inertia of the disc is negligible.

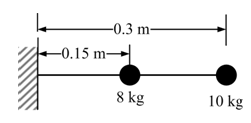
Figure E8.2

Exercise 8.3 For Exercise 8.2 when the left and right discs have respectively diametral mass moment of inertias as I_d1 = 0.05 kg-m² and I_d2 = 0.06 kg-m² , obtain the transverse natural frequencies and mode shapes of the rotor system. [ Hint : Use the eigen value formulation for the present case]

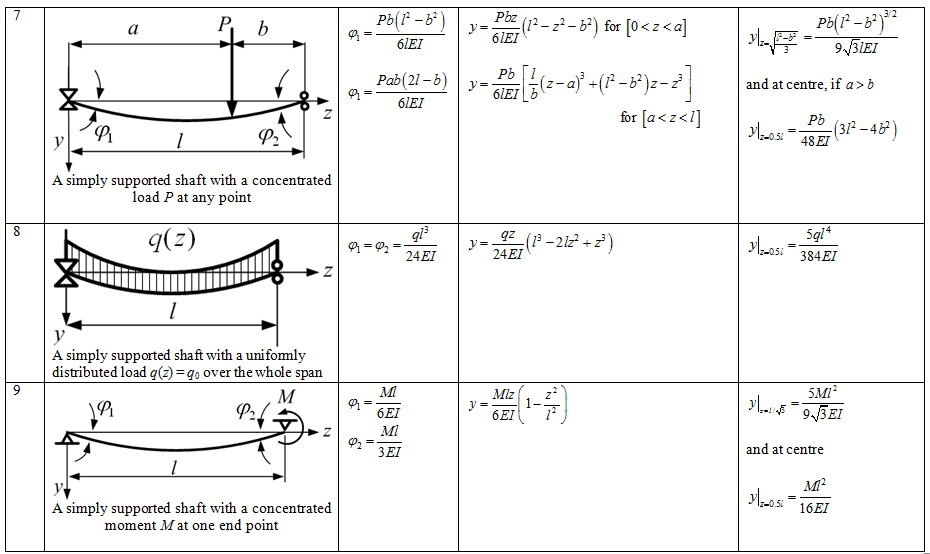
Exercise 8.4 Obtain the transverse natural frequency of a rotor system as shown in Figure E8.4. The mass of the disc m , is 5 kg and the diametral mass moment of inertia, I_d , is 0.02 kg-m² . Shaft lengths are a = 0.3 m and b = 0.7 m. The diameter of the shaft is 10 mm.

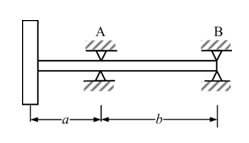
Figure E8.4 An overhang rotor system