For second branch, i.e., equation (b) and noting equation (m), we have

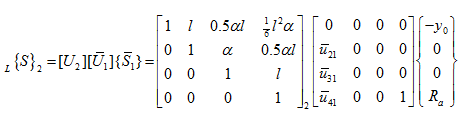(n)

On simplifying equation (n), we get

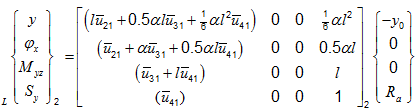(o)

On expanding equation (o), we have

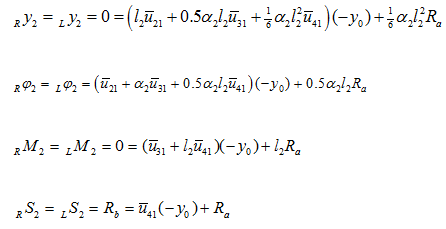(p)

From equation (p) the first equation, we have

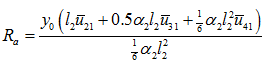(q)

On substituting equation (q) in the third equation of set of equations (p), and noting that since y₀ ≠ 0, we get

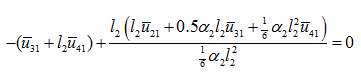(r)

On simplification of equation (r), we get

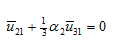(s)

which is the frequency equation. On substituting variables defined in equation (l) into equation (s), we have

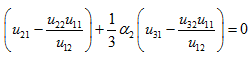(t)

In view of variables defined in equations (g) and (h), the frequency equation (t) becomes

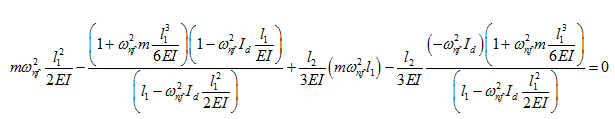
which can be simplified as

(u)

For the present problem, we have

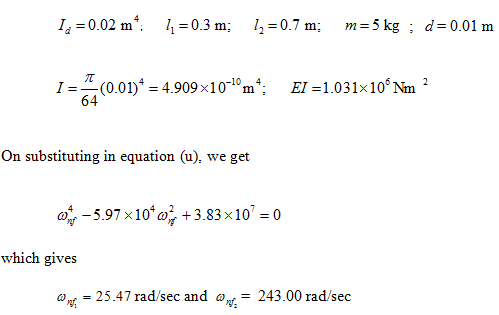
The mode shapes can be obtained by using transfer matrices between various intermediate stations derived in equations (q), (p), (o), (m), (b) and (a). For a reference y 0 = 1 may be chosen. This is left to readers as an exercise.

Alternative method for the above example is explained now. A transformation matrix to transform the state vector from the left of a support to the right of the support can be developed as follows (refer equation (d)):

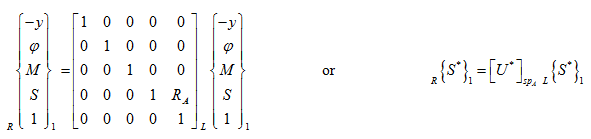(v)