where now all vectors and matrices are modified to accommodate the reaction force from the support. Modifying all other transformation in equations (a) and (b), we get the modified overall transformation as
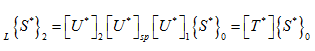 |
(w) |
which can be expanded as
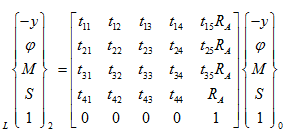 |
(x) |
Boundary conditions given in equations (c) and (e), can be applied in equation (x) to get
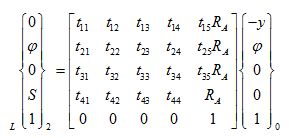 |
(y) |
which gives
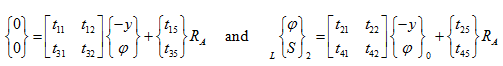 |
(z) |
The first of equation (z) can be rearranged as
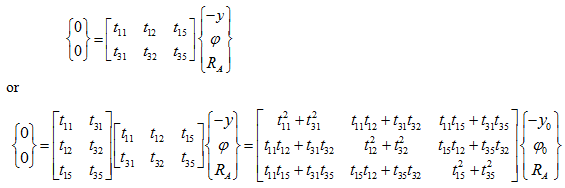 |
(a1)
(b1) |
For the non-trial solution of equation (b1), we should have
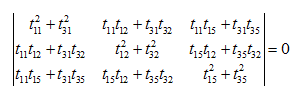
It can be verified that equations (b1) and (u) will be identical. It should be noted that the transformation between the right and left side of the support B can be written as
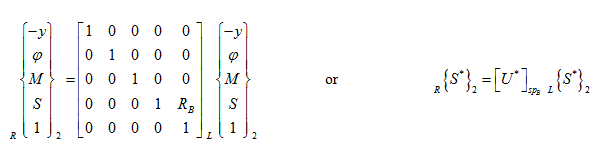 |
(a1) |
which will be used for getting the state vector in the right of support B.
Answer .
Example 8.9 Obtain the variation of the transverse natural frequency with the shaft speed (i.e., obtained the Campbell diagram) of an overhang rotor system as shown in Figure 8.36. From such Campbell diagram obtain critical speeds. The end B1 of the shaft is having fixed end conditions. Length of the shaft is 0.2 m and diameter is 0.01 m. The disc is thin and has 1 kg of mass and the radius of the disc is 3.0 cm. Consider gyroscopic effects, however, neglect the mass of the shaft. Take the range of the shaft speed such that it covers at least two critical speeds in the Campbell diagram. Use the TMM.
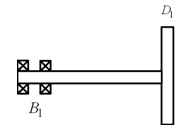
Figure 8.36
Solution : Because of gyroscopic effect now the motion in the two orthogonal planes will be coupled. This requires considering the modified field and point transfer matrices as given by equations (8.35) and (8.47). In additional, the gyroscopic effect will introduce the following new terms in the point matrix: P*3,14 = − P*7,10 = − P*11,6 = P*15,2 = Ipωv, where subscripts represent the row and column, respectively, in the modified point matrix and ω is the spin speed of the shaft. Let station 0 be the fixed end and station 1 be the free end. For free vibrations, then the overall transformation can be written as
 |
(a)
(b)
(c)
(d)
(e)
(f)
(g) |