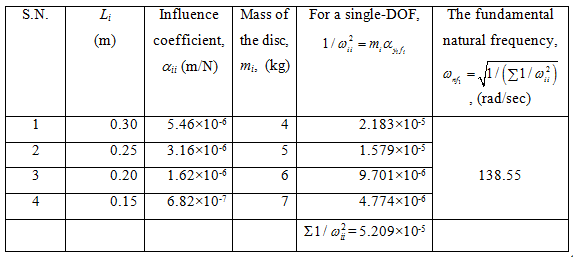
We have d = 0.02 m, and EI = 1649.34 N-m² . Table 8.7 summarises the calculation of the fundamental natural frequency.

Table 8.7 Calculation procedure of the fundamental natural frequency using the Dunkerley 's formula

Answer .

Concluding Remarks:

To summarise, in the present chapter we studied methods of calculation of natural frequencies and forced responses. Two main methods namely, the influence coefficients and transfer matrix methods, are given detailed treatment. The Durkerley's formula for the approximate estimation of the fundamental frequency is presented. All three methods are illustrated with simple examples keeping calculation complexity to a minimum, while retaining various basic features of the solution method for a variety of cases. The application of these methods for larger system is then straight forward; however, it requires help of computer. The influence coefficient method is simple in application; however, it requires calculations of influence coefficients with the help of load-deflection relations, which are different for different systems. Moreover, with number of DOF of the system the matrix size increases, so it requires higher computational time for large rotor systems to solve the eigen value problem. The transfer matrix method is quite systematic and effective even for multi-DOF systems. It does not require any a prior calculation of the system matrix element as in the influence coefficient method. The overall size of the matrix remains the same, and it does not increase with the DOF of the system. However, for the calculation of natural frequencies, this method requires roots searching numerical method, which is time consuming and there is risk of missing some roots. The dynamic matrix method (not described here) is similar to the TMM in that it relates to the state vectors at different stations, however, while assembling the components equations the size of the matrix no longer remains the same and it increases with the DOF of the system. In fact, the finite element method is the improvised version of this method as we will see in the next chapter.

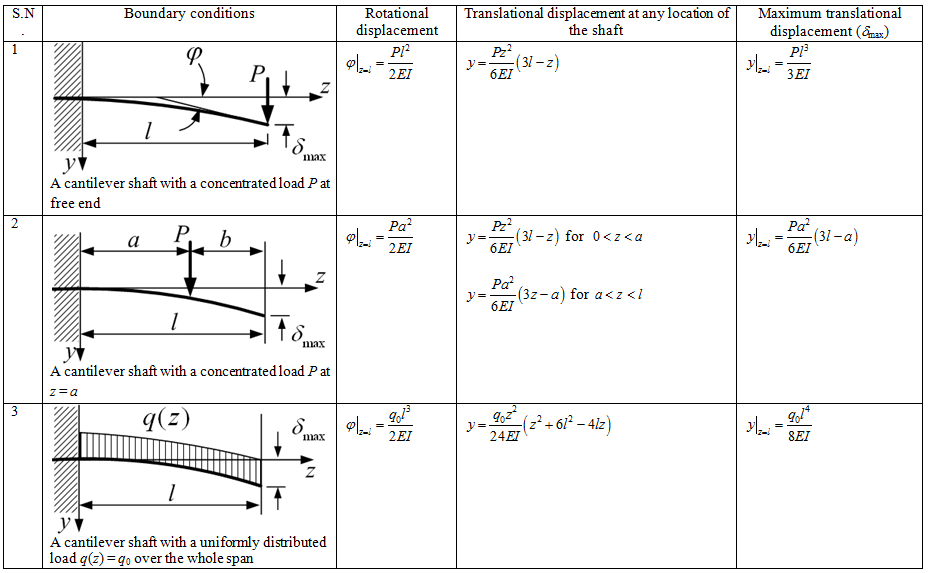
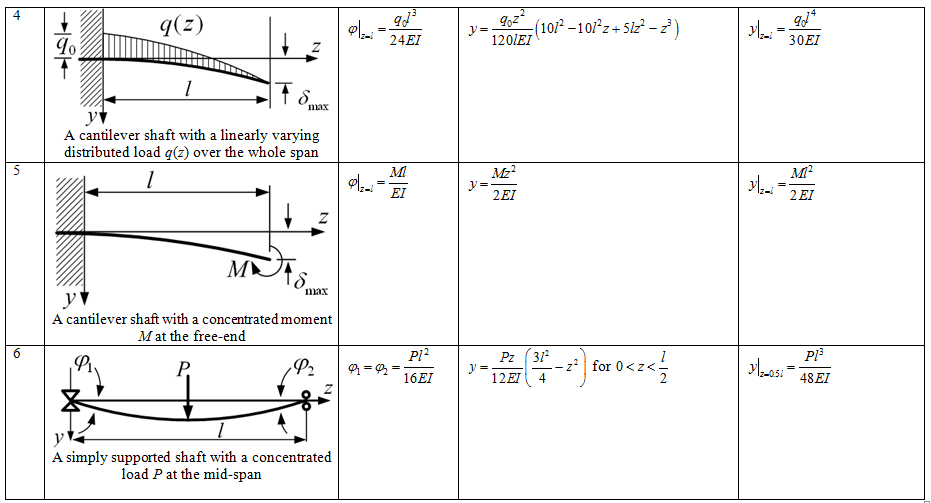
Appendix 8.1 Load deflection relations for various boundary conditions of the shaft