8.3 Dunkerley's Formula
Dunkerley's formula can be used to calculate the fundamental transverse natural frequency without the help of the numerical methods. This method gives very rough estimation of natural frequency. From the influence coefficient method, the natural frequency of the system is obtained by the following conditions
(8.69) |
For two degrees of freedom system by considering only the translational displacements, the above equation will be of the following form
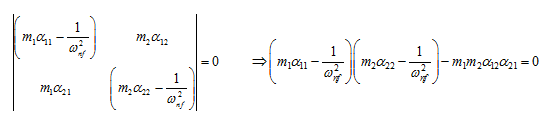
which can be rearranged as
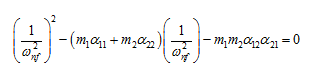 |
(8.70) |
but for a polynomial whose first coefficient is unity, the second coefficient is equal to minus of the sum of the roots of the equation (Scarborough, 1966)
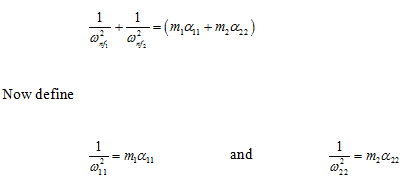 |
(8.71)
(8.72) |
where ω11 and ω22 are natural frequencies of single-DOF system , respectively, when mass m 1 alone is present and when mass m 2 alone is present. Hence, we have
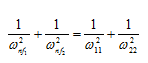 |
(8.73) |
It can be proved that in general for multi-DOF systems, we can write
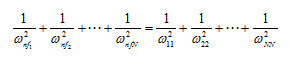 |
(8.74) |
where N is the total DOFs of the rotor system. In most cases the fundamental frequency ωnf1 will be much lower than the all other higher natural frequencies, so the above equation may be written as
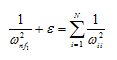 |
(8.75) |
where ε is a small positive quantity. The above equation can be rearranged as
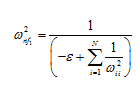 |
(8.76) |
On neglecting ε, we can find the fundamental natural frequency of the rotor system, as
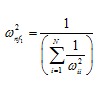 |
(8.77) |
It should be noted that since e is a positive quantity, the we will get a lower bound of the fundamental frequency from the present method as opposed to FEM in which we always get higher bounds of natural frequencies.
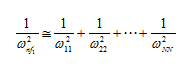 |
(8.78) |
Dunkerley first suggested this. Equation (8.78) always gives a value for fundamental frequency, which is slightly lower than the true value, by virtue of the approximation involved. There are other approximate methods are available that can be used to obtain bounds of natural frequencies of the rotor system for example the Rayleigh's quotient (Meirovitch, 1986).
Example 8.10 Find transverse natural frequencies and mode shapes of a rotor system shown in Figure 8.43. B is a fixed end, and D1 and D2 are rigid discs. The shaft is made of the steel with the Young's modulus E = 2.1 × 1011 N/m2 and a uniform diameter d = 10 mm. Shaft lengths are: BD2 = 50 mm, and D1D2 = 75 mm. The mass of discs are: m1 = 2 kg and m2 = 5 kg. Consider the shaft as massless and neglect the diametral mass moment of inertia of discs.
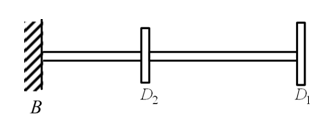
Figure 8.43
Solution : For Figure 8.43, we have
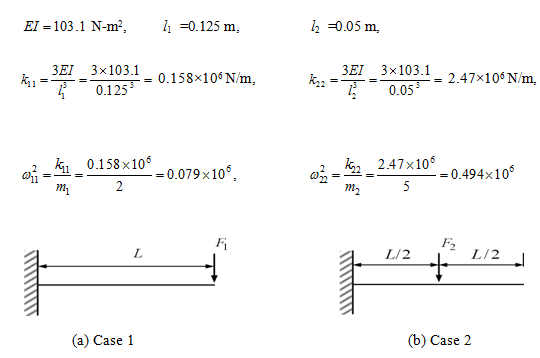
Figure 8.44 Overhang rotor systems with a single disc