These state vectors for the fundamental natural frequency are summarized in Table 8.5(a). The mode shape for the translational and rotational displacements are extracted for Table 8.5(a) and are drawn as sho wn in Fig. 8.33(a) and (b), respectively. On the same lines other state vectors corresponding to va rious natural frequencies can be obtained and are given in Table 8.5(b-h) and corresponding mode shapes from 2nd to 5th modes are shown in Fig. 8.33(c-d).
Table 8.5(a) Relative values of state vectors at various stations for the fundamental natural frequency
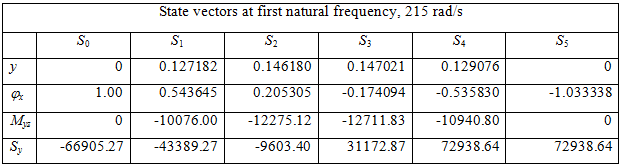
Table 8.5(b) Relative values of state vectors at various stations for the second natural frequency
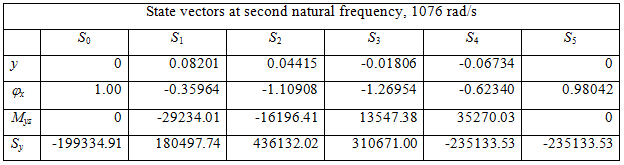
Table 8.5(c) Relative values of state vectors at various stations for the third natural frequency
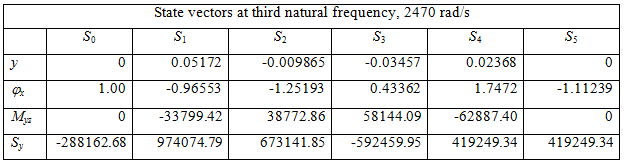
Table 8.5(d) Relative values of state vectors at various stations for the fourth natural frequency
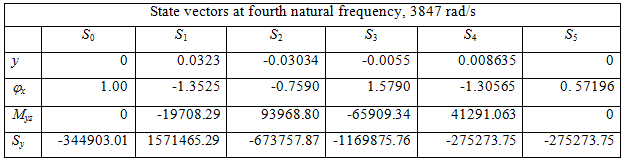
Table 8.5(e) Relative values of state vectors at various stations for the fifth natural frequency
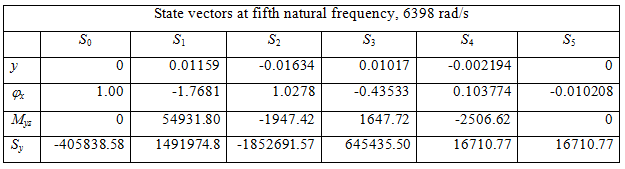
Table 8.5(f) Relative values of state vectors at various stations for the sixth natural frequency
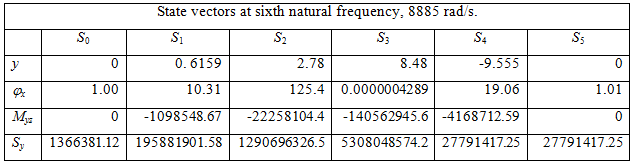
Table 8.5(g) Relative values of state vectors at various stations for the seventh natural frequency
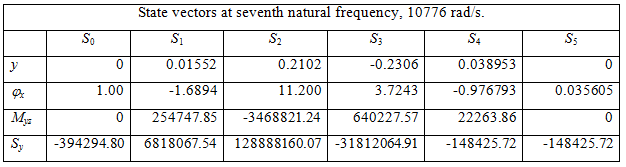
Table 8.5(h) Relative values of state vectors at various stations for the eighth natural frequency
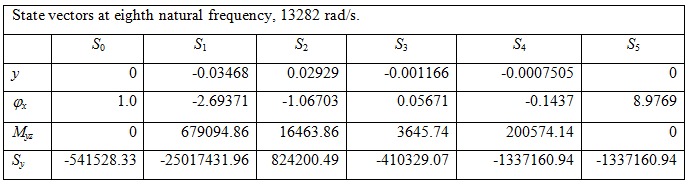
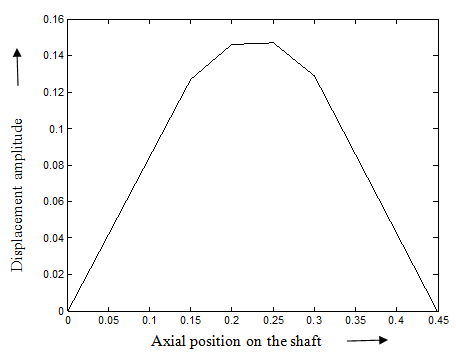
Fig. 8.33(a) The fundamental mode shape of translational displacements