and

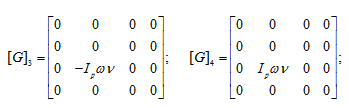
Example 8.4 Obtain the unbalance response and transverse critical speeds of an overhang rotor system as shown in Figure 8.23. End B₁ of the shaft is fixed. The length of the shaft is 0.2 m and the diameter is 0.01 m. The disc is thin and has 1 kg of mass with the radius of 3.0 cm. Neglect the mass of the shaft and the gyroscopic effect. Take an unbalance of 3 gm at a radius of 2 cm. Choose the shaft speed suitably so as to cover two critical speeds in the unbalance response. E = 2.1 × 10¹¹ N/m² .

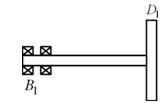
Figure 8.23

Solution : Let station 0 be the fixed end and station 1 be the free end. Consider only a single plane motion. The overall transformation can be written as

(a)   (b)   (c)       (d)

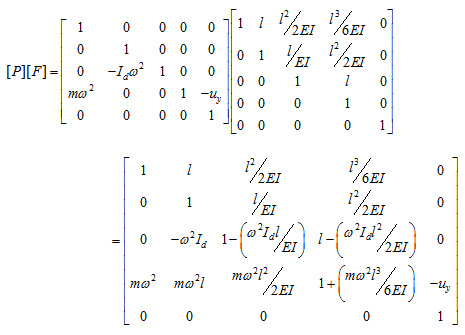(e)

Boundary conditions for the present case are that all the translational and rotational displacements at station 0 are zero and all the moments and shear forces are zero at right of station 1. Hence, the state vector at the station 0 and right of 1 will have the following form

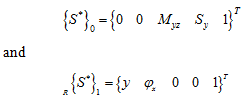(f)   (g)

From free vibrations, unbalance, u_y , is zero. Hence, 3^rd and 4^th rows will give the eigen value problem of the following form

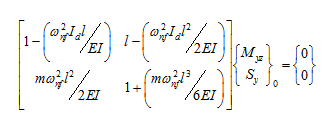(h)

which gives a polynomial of the following form

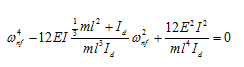(i)

For the present problem, we have following data

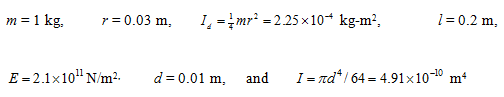
Hence from equation (i), we get

which gives natural frequencies as