8.2.6 Gyroscopic effects: If gyroscopic effects are allowed for, in equation (8.47) the modified point matrix, [P *], will get some extra terms, however, the modified field matrix, [F *], will not be affected. For free vibrations, the formulation would have more general form since equations will contain both the natural whirl frequency, v (while considering gyroscopic effects we tried to distinguish the whirl natural frequency symbol by v in place of ω_nf; while the former is speed-dependent v(ω), the latter is speed independent so that v(ω = 0) = ω_nf), and the spin speed, ω , of the shaft. This leads to speed dependency of the natural whirl frequency.

Equilibrium equations for the moment in the y - z vertical and z - x horizontal planes, considering gyroscopic moments also, are given as (noting equation (8.39) and for gyroscopic terms refer Chapter 5)

(8.60)

and

(8.61)

where I_p is the polar mass moment of inertia of the disc. In the modified matrix [P *], following rows and columns element will be affected: (i) Equations (8.60) and (8.61) are equations of moments, and in the state vector {S }, 3^rd , 7^th , 11^th and 15^th rows are for moment equations. Hence, only these rows in the modified matrix [P *] will be affected. Now in equations (8.60) and (8.61), additional terms for slopes, φ_y and φ_x (see Figure 8.22), are appearing because of gyroscopic effects. In the modified state vector {S *} the rotational displacements are at 2^nd , 6^th , 10^th and 14^th rows. Hence in the modified point matrix [ P * ] columns 2^nd , 6^th , 10^th and 14^th will be affected. For more clarity of the above explanation let us express rotational displacements and moments as

(8.62)

where V be the natural whirl frequency with gyroscopic effects, and subscripts r and j represent the real and imaginary parts of a complex quantity, respectively (for brevity the subscript i corresponding to i ^th mass has been dropped). On substituting equation (8.62) into equation (8.60), we get

(8.63)

Separating the real and imaginary parts from equation (8.63), we get

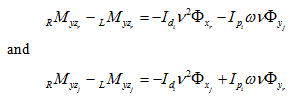(8.64)   (8.65)

It should be noted that equation (8.64) corresponds to 11^th row in equation (8.47) and gyroscopic effects term (i.e., −I_ptωv, which is the coefficient of φ_yj that is in the 6^th row of the modified state vector {S *}) in equation (8.64) will corresponds to 6^th column in equation (8.47). Similarly, from equation (8.65), it can be seen that gyroscopic effects will introduce another term (i.e., I_ptωv) at 15^th row and 2^nd column corresponding to M_yzj and φ_yr , respectively. Hence, we have

(8.66)

where P_{i, j} represent the additional element at the i ^th row and the j ^th column of the modified point matrix.

Similarly, using equation (8.61), we get the additional element of the modified point matrix as

(8.67)

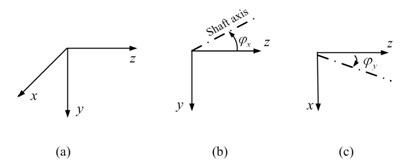
Figure 8.22 Coordinate axes and positive conventions for rotational displacements (a) Rectangular 3-dimensional axis system (b) tilting of the shaft axis in z - x plane (c) tilting of shaft axis in y - z plane

Hence, the modified point matrix with gyroscopic effect would relate state vectors in either side of i ^th disc as follows (refer Eqn. (8.47))

(8.68)