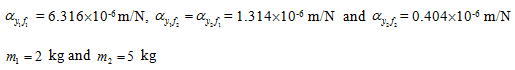On evaluating the deflection at station 1 for z = 0 (i.e., at the free end), we have

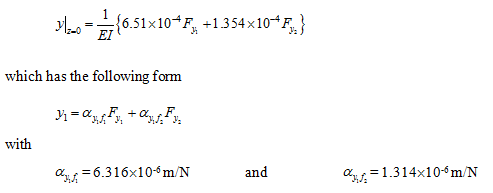
The deflection at station 2 for z = 0.075 m, we get

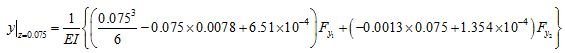(s)

which has the following form

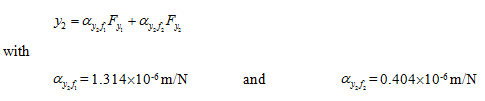
which is same as obtained by the energy method.

Tabular method from deflection relations :

For a force f_y at a distance a from the free end of a cantilever beam, the transverse deflection can be written as

where L is the total span of the beam and z is measured from the free end. Let the force f_y1 is acting at free end and the force f_y2 is acting at a distance a from the free end. Let l₁ and l₂ are distances from fixed end to the force f_y2 and from the force f_y2 to the force f_y1 , respectively. Then, influence coefficients can be defined as

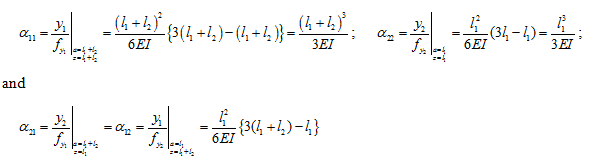
Table 8.1 shows the systematic calculation of influence coefficients. For the present case in fact the last column is of interest and it can be seen that these values of influence coefficients are matching with the previously obtained influence coefficients.

Table 8.1 Calculation of influence coefficients from deflection relations

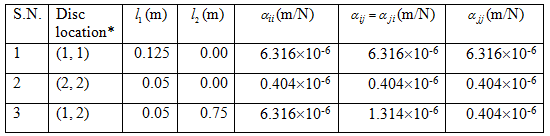
* Numbers in bracket represent force station numbers (e.g., for first two serial nos. single force is represent, respectively, at station 1 and 2, and for the third serial no. two forces are present at stations 1 and 2 both).

For free vibrations from equation (8.17), we have

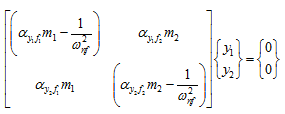(t)

For a non-trial solution, it gives

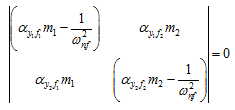(u)

which give the frequency equation as

(v)

For the present problem, we have