Equation (e) has the following form

(f)

Hence, for a = 0.075 m, L = 0.125 m, N-m² , we have

(g)

The deflection at station 2 can be obtained as

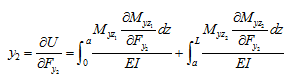(h)

On substituting equations (a) and (b) into equation (h), we get

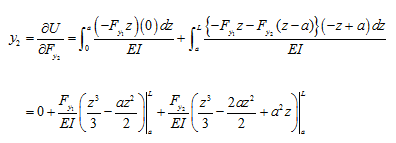
which finally takes the form

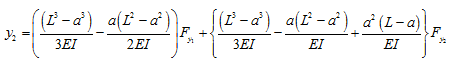(i)

Equation (i) has the following form

(j)

Hence, for a = 0.075 m, L = 0.125 m, EI = 103.1 N-m² , we have

(k)

Method of the singularity function : Now the influence coefficients are obtain by the method of singularity function for illustration. The singularity function (< >) is defined as

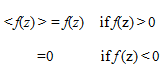(l)

The bending moment at any cross-section along the shaft span can be written as

(m)

which implies that for 0 ≤ z ≤ a contribution from the F_y2 would not be there since ( z – 0.075) would be a negative quantity so it becomes zero. However, for a ≤ z ≤ L contributions from both F_y1 and F_y2 would be there. On integrating twice equation (m), we get following expressions

(n)

and

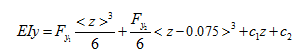(o)

where the integration constants c₁ and c₂ are obtained by boundary conditions of the probelm, and are give as

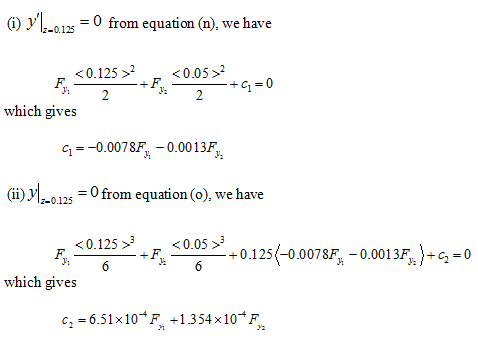(p)         (q)

Finally equation (o) becomes

(r)