In view of equation (8.9), equation (8.15) can be rearranged as
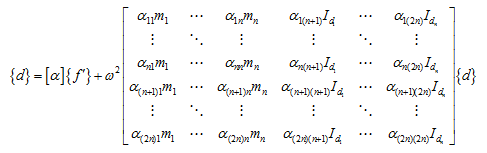 |
(8.16) |
which can be written in more compact form as
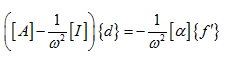 |
(8.17) |
with
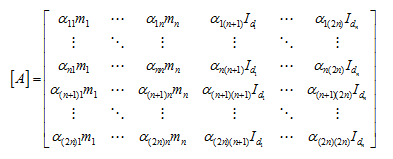 |
(8.18) |
Disc displacements x and φy can be calculated for known applied loads (e.g., the unbalance forces and moments) as
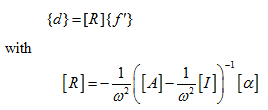 |
(8.19)
(8.20) |
where R represents the receptance matrix and for the present case it contains only real elements. For free vibrations the right hand side of equation (8.17) will be zero and ω = ωnf , i.e.
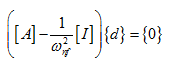 |
(8.21) |
which only satisfy when
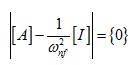 |
(8.22) |
and it will give the frequency equation and system natural frequencies could be calculated from this. Alternatively, through eigen value analysis of matrix [ A ] system natural frequencies and mode shapes could be obtained directly.
In general, the receptance matrix, [ R ] , may contain complex elements when damping forces also act upon the shaft, in which case applied forces and disc displacements will not all be in phase with one another. Hence, a more general form of equation (8.19) would be that which indicates both the real and imaginary parts of x , f´and R . In such case the real and imaginary parts of each equations need to be separated and then these can be assembled again to into a real matrix form , which will have double the size that with complex quantities. Some of the steps are described below
![]()
where r and i refer to the real and imaginary parts, respectively. Above equation can be expanded as
![]()
Now on equating the real and imaginary parts on both sides of equations, we get
![]()
Above equations can be combined again as
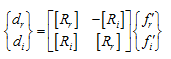 |
(8.23) |
It can be observed that now the size of the matrix and vectors are double as that of equation (8.19). It should again be noted that the present analysis is only for one plane motion and for two plane motion the size of the matrix would be double of the matrix size in eqn. (8.23). Now through simple numerical examples (for the two or more DOFs) some of the basic concepts of the present method will be illustrated.