Hence, now the next step would be to obtain the influence coefficient, α11. Using the energy method this influence coefficient is obtained as follows (refer Timoshenko and Young (1968) for more detail about the method)
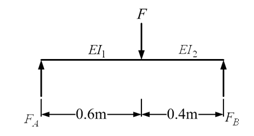
Figure 8.5 A free body diagram of the rotor system
For a load F when it acts at the disc, reaction forces at bearings can be obtained as (Figure 8.5)
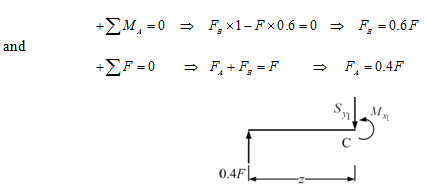
Figure 8.6 Free body diagram of the shaft section 0 ≤ z ≤ 0.
From Figure 8.6, the bending moment in the shaft can be obtained as
(a) |
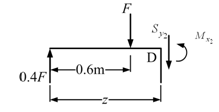
Figure 8.7 Free body diagram of the shaft section 0.6m ≤ z ≤ 1.0m.
From Figure 8.7, the bending moment in the shaft can be obtained as
(b) |
The strain energy stored in the shaft from bending moments can be obtained as
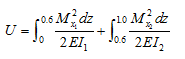
From the Castigliano's theorem the translational displacement can be obtained as
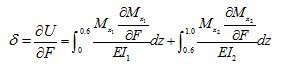 |
(c) |
On substituting equations (a) and (b) into equation (c), we get
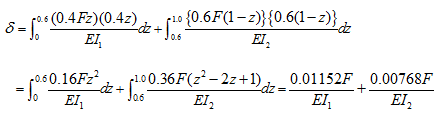
The stiffness of the beam given as
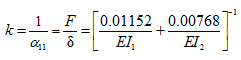
From above in fact it can be observed that two shaft segment can be thought as connected parallel to each other at disc location.
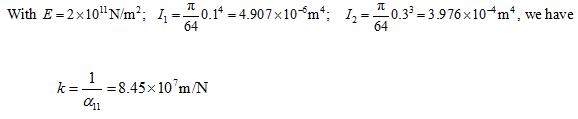
Hence the natural frequency is given as
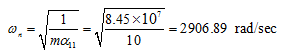
The influence coefficient can be also obtained by the singular function approach and for more details readers are referred to Timoshenko and Young (1968).