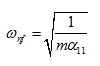Example 8.1 Obtain transverse natural frequencies of a rotor system as shown in Figure 8.3. Take the mass of the disc, m = 10 kg and the diametral mass moment of inertia of the disc, Id = 0.02 kg-m2 . The disc is placed at 0.25 m from the right support. The shaft has a diameter of 10 mm and a span length of 1 m. The shaft is assumed to be massless. Take the Young's modulus E = 2.1 × 1011 N/m2 of the shaft. Consider a single plane motion only. Compare the results for the case when the disc is at mid-span.
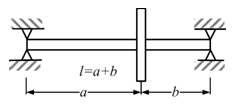
Figure 8.3 A rotor system
Solution : Influence coefficients for a simply supported shaft are defined as
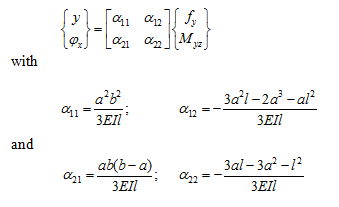
It should be noted that subscript 1 represents corresponding to a force or a translational displacement, and subscript 2 represents a moment or an rotational displacement. To obtain natural frequencies of the rotor system having a single disc, from equation (8.21), we have
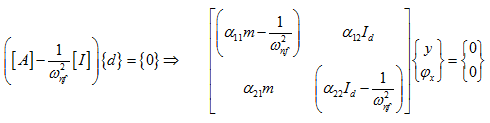 |
(a) |
Hence, the determinant of the above matrix would give the frequency equation as
(b) |
For the present problem, we have
![]()
Equation (a) becomes,
![]()
which gives two natural frequencies of the system, as
It should be noted that the translational and rotational motions are coupled for the present transverse vibrations since the disc is offset from its mid span; however, when the disc is at the mid span then the translational and rotational motions will be decoupled (i.e., α12 = α21 = 0). Natural frequencies for such case would be ![]()
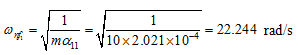 |
(d) |
for the pure translation motion of the disc, and
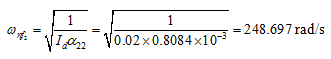 |
(e) |
for the pure rotational motion of the disc. These expressions (d) and (e), also of course, can be obtained from frequency equation (a) for α12 = α21 = 0.
Example 8.2 Find the transverse natural frequency of a stepped shaft rotor system as shown in Figure 8.4. Consider the shaft as massless and is made of steel with the Young's modulus, E = 2.1 (10)11 N/m2 . The disc could be considered as a point mass of 10 kg. The circular shaft is simply supported at ends (In Figure 8.4 all dimensions are in cm).
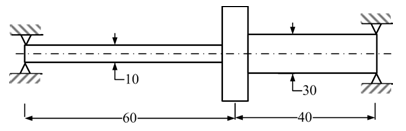
Figure 8.4 A simply supported stepped shaft
Solution : To simply the analysis let us consider that the rotational displacement of the disc is negligibly small. From equation (8.23), we have
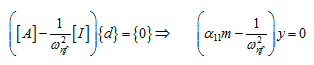
from which the natural frequency is given as