Figure 8.16 shows a cantilever shaft with a force at station 2, and has a station 3 between the force and the fixed end. Between two stations, it will have the following influence coefficients
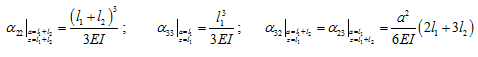 |
(c) |
These relations could also be used between stations (2, 4) and (3, 4).
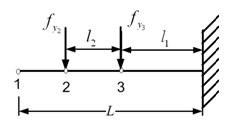
Figure 8.16 A cantilever shaft with two forces intermediate stations
Table 8.2 A calculation procedure of influence coefficients in a multi-discs cantilever shaft
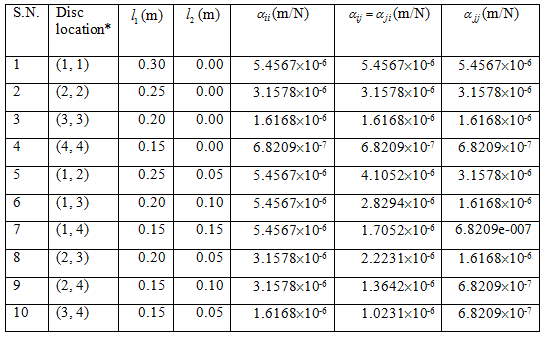
* Numbers in bracket represent the force station numbers
It should be noted that in Fig. 8.16 the shaft segment from the force fy2 to the free end would act as rigid shaft. It will not contribute in the deformation of the shaft at station 2, and it will act as if it is not present at all (this is true only for mass-less shaft assumption).
For example, when discs 1 and 2 are present, we have l1 = 0.25 m and l2 = 0.05 m. Hence, the influence coefficients from eqn. (a) take the following form: α11 = 5.4567 × 10−6 m/N, α12 = α21 = 4.1052 × 10−6 m/N, α22 = 3.1578 × 10−6 m/N. Similarly, when discs 2 and 3 are present, we have l1 = 0.20 m and l2 = 0.05 m. Hence, the influence coefficients from eqn. (b) take the following form: α22 = 3.1578 × 10−6 m/N, α23 = α32 = 2.2231 × 10−6 m/N, α33 = 1.6168 × 10−6 m/N. On the similar lines other influence coefficients can be calculated and it is summarized in Table 8.2
Now for free vibrations, the governing equation has the following form
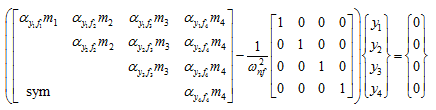 |
(d) |
which can be written as for the data of the present problem, as
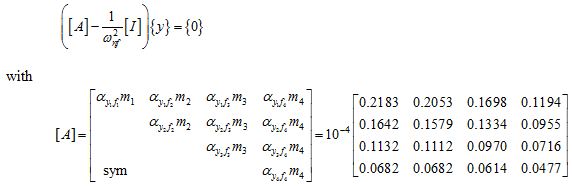 |
(e) |
The eigen value and eigen vector of the above matrix is obtained as
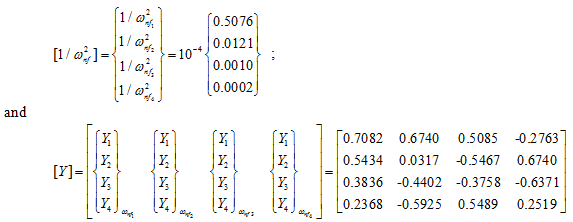
Hence, the transverse natural frequencies are
![]()
The corresponding eigen vectors (mode shapes) can be plotted. It should be noted that in the eigen vector matrix, [ Y ], the first column components have no sign change that is corresponding to the fundamental mode, however, in subsequent columns, i.e. 2, 3 and 4, there are sign changes and for each sign change there would be a node in that particular mode (i.e., for the second mode there is a node between station 2 and 3 (single node), for the third mode there are nodes between stations 1 & 2 and 3 & 4 (two nodes), and finally for the fourth mode there are nodes between stations 1 & 2, 2 & 3, and 3 & 4 (three nodes).
Answer