Example 8.3 Find transverse natural frequencies and mode shapes of a rotor system shown in Figure 8.8. B is a fixed end, and D₁ and D₂ are rigid discs. The shaft is made of the steel with the Young's modulus E = 2.1 × 10¹¹ N/m² and a uniform diameter d = 10 mm. Shaft lengths are: BD₂ = 50 mm, and D₁D₂ = 75 mm. The mass of discs are: m₁ = 2 kg and m₂ = 5 kg. Consider the shaft as massless and neglect the diametral mass moment of inertia of discs.

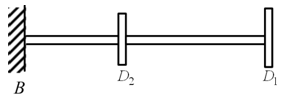
Figure 8.8

Solution : For simplicity of the analysis, the shaft is considered as massless and disc masses are considered as point masses (i.e., the diametral mass moment of inertia of discs are neglected that means rotational displacements are ignored). The first step would be to obtain the influence coefficients corresponding to two disc locations acted by concentrated forces. Basically, we need to derive translational displacements at two disc locations due to forces F₁ and F₂ acting at these locations as shown in Fig. 8.9. These deflection relations are often available in a tabular form in standard handbooks (e.g., Young and Budynas, 2002). However, for the present problem the calculation of influence coefficients is explained by the energy method and by the singularity function to clarify the basic concept of the procedure for the completeness in case standard handbook is not available for a particular case.

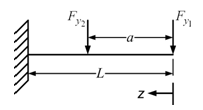
Figure 8.9 A shaft with two concentrated forces

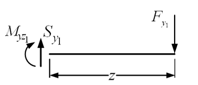
Fig. 8.10 The free-body diagram of a shaft segment for 0 ≤ z ≤ a

Energy method : In this method, we need to obtain the strain energy due to bending moments in the shaft. Bending moments at different segments of the shaft can be obtained as

1. Shaft segment for 0 ≤ z ≤ a

From Fig. 8.10, the bending moment can be written as

(a)

2. Shaft segment for a ≤ z ≤ L

   From Fig. 8.11, the bending moment can be written as

(b)



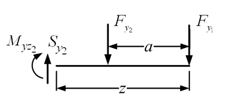
Fig. 8.11 The free-body diagram of a shaft segment for a ≤ z ≤ L

The total strain energy is given by

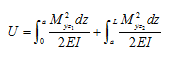(c)

Using the Castigliano theorem, the translational deflection at station 1 can be written as

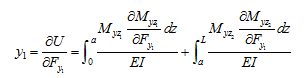(d)

On substituting equations (a) and (b) into equation (d), we get



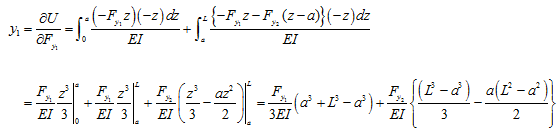
which finally takes the form

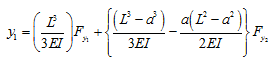(e)