The change in the lubricant film forces are then given by

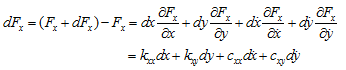(3.99)

and

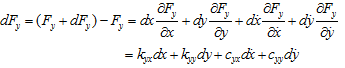(3.100)

where k_ij and c_ij are known as the fluid-film stiffness and damping coefficients respectively, and i and j can take values of x and y. These bearing dynamic coefficients must be known in order to calculate the overall system dynamic response to an external forcing, and its stability. Values of k_xx and k_yx can be found from the Reynolds equation by calculating the lubricant film forces and when a small displacement dx is imposed on the journal (from its static equilibrium position) with dy, and  all set to zero. The process is then repeated with a displacement of – dx to calculate and . The stiffness coefficientsk_xx andk_yx are then given by

(3.101)

Similarly, values of the other stiffness and damping coefficients may be evaluated by imposing small variations in dy, and  on the journal one at a time, and investigating their effect on the lubricant film forces, as

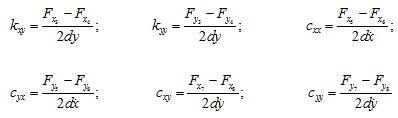(3.102)

It should be noted that when proceeding in the manner described above care should be taken when formulating Reynolds equation (3.79) in the finite difference form, as the quantity ∂h/∂t is no longer zero when  or are non-zero, and appropriate value of U is also dependent on and . Solutions for several types of bearing have been carried out (Lund et al., 1965; Homer, 1960, Someya, 1988). In addition to the ‘spring’ and ‘damping’ coefficients introduced above, some authors have suggested the use of ‘inertia’ coefficient and ‘moment’ coefficients. Although such coefficients usually have only a small effect on bearing dynamics. Inertia coefficients can be defined as

(3.103)

For perturbations in displacements, velocities, and accelerations, we have

(3.104)

where m_ij is the inertia coefficients. Moment coefficients can be defined as

(3.105)

For perturbations in the linear and angular displacements, velocities, and accelerations, we have

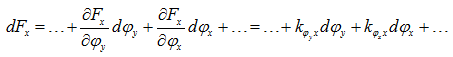(3.106)

and

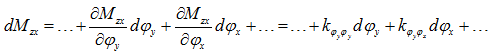(3.107)

where  are moment stiffness coefficients.