The equation remains applicable with non-circular bore of the bearing.
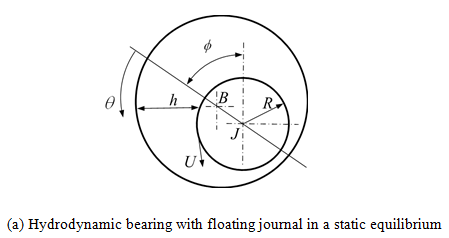
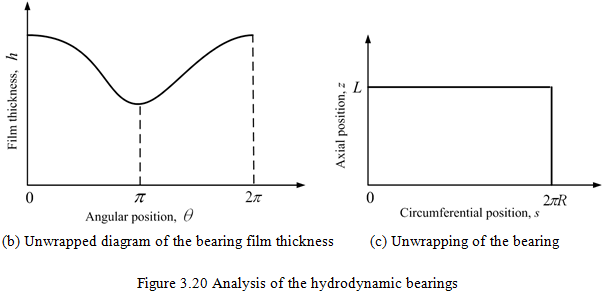
3.2.3 Basic concepts and assumptions of fluid-film bearing models
For a given bearing and rotational speed, lubrication theory may be used to calculate the reaction forces on the journal from the lubricant film. These forces are functions of the displacements of the journal from bearing center, and of the instantaneous journal center velocities and accelerations. Hence, for small amplitude motions, measured from the static equilibrium position (see Figure 3.21) of the journal (u0, v0), a first order Taylor series expansion of fluid force functions yield (more detailed steps would be provided in subsequent sections)
 |
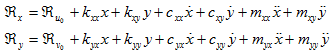(3.80) |
where
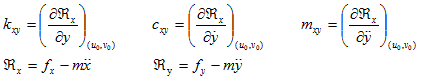
and analogously the remaining bearing dynamic coefficients may be defined. In the matrix form of equation (3.80) all diagonal terms are called direct coefficients and off-diagonal terms are called cross-coupled terms. The latter terms arise due to the fluid rotation within the bearing. 
is the reaction force of fluid film on the journal, f(t) is the external excitation force on the journal, m is the journal mass, u0 andv0 are the static equilibrium position of the journal from the bearing center, x and y are the displacements of the journal from its static equilibrium position, 
are the instantaneous journal center velocities and 
are the instantaneous journal center accelerations, in the horizontal and vertical directions, respectively. The “dot” indicates the time derivatives and kij, cij and mij (i, j = x, y) are bearing stiffness, damping and added-mass (also termed the virtual fluid-film mass or inertia) coefficients respectively. The indices of the stiffness, damping and added-mass coefficients have the following significance: the first index gives the direction of loading which produces the elastic (damping/inertia) force and the second index gives the direction of the displacement (velocity/acceleration). Because (u0, v0) is the equilibrium position, then 
equals the static load, W.
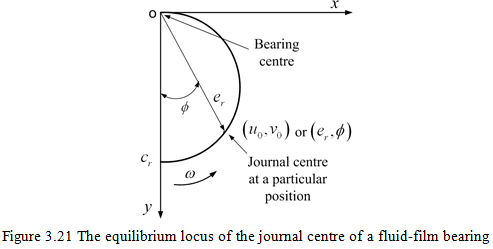
The equilibrium position depends on a unique value of the dimensionless Sommerfeld number, S = (µωRL/W)(R/cr )2(L/D)2, where µ is the lubricant viscosity, ω is the journal rotational speed, D is the bearing bore, R is the journal radius, L is the bearing length and cr is the bearing radial clearance. The Sommerfeld number, S, defines the operating conditions (speed, lubricant viscosity, static load, and geometry). The dynamic coefficients are evaluated for a particular static equilibrium position, which is a function of the Sommerfeld number, S, which means that for a given application, they are functions of rotor speed. Moreover, bearing dynamic coefficients could be the external excitation frequency, Ω, dependent.
It should be noted that equation (3.80) is a complete form of linearised fluid-film dynamic equation and it contains twelve stiffness, damping and added-mass coefficients. Consistent with the assumptions inherent in reducing the Navier-Strokes equations to the Reynolds equation, the conventional laminar, thin film lubrication theory ignores the inertia forces in the fluid-film (Pinkus and Sternlicht, 1961; Schlichting, 1960). This is theoretically justified for small values of the Reynolds number (of the order of 1). On the other hand, the assumption of laminar flow ceases to be valid when there is transition to either Taylor vortex flow or to turbulent flow which, for fluid-film cylindrical journal bearing, occurs at a Reynolds number of approximately 1000 to 1500. Thus, there is an intermediate range, say for values of Reynolds number of the order of 100, where added-mass effects may become noticeable (several times more than the mass of the journal itself) without affecting the assumption of laminar flow. The added-mass coefficients represent the mass of the bearing fluid-film (Reinhardt and Lund, 1975) but are significant only in exceptional cases and in most analyses the added-mass of the bearing film are ignored. The stiffness and damping coefficients can be obtained by a finite difference solution of the perturbed Reynolds equation (Lund and Thomsen, 1978).
From the lubrication theory (ignoring inertia effects) damping coefficients are symmetric but stiffness coefficients are not. Therefore, principal directions do not exist (although this was assumed by Hagg and Sankey (1956) and Duffin and Johnson (1966-67)), and in the experimental determination of the coefficients, it is necessary to obtain two independent sets of amplitude-force measurements. Lund (1987) emphasized the experimental measurement of the bearing coefficients and established more uniform agreement with analytical calculations by considering the influence of thermal and elastic deformations and practical problems of manufacturing and operating tolerances of bearing geometry, clearance and lubricant viscosity. Although the load-displacement characteristics of a journal bearing is evidently non-linear, the concept of linear dynamic coefficients is still used for modern rotor dynamic calculations for unbalance response, damped natural frequencies, and stability since experience has demonstrated the usefulness of the coefficients. Clearly the applicability of these techniques is dependent on small amplitudes of vibration at the journal (relative to the bearing clearance).