For a especial case Φ = v/2 (i.e., when the radial load is passing through bisector of the two neighbouring rolling elements) and y = 0 (i.e., the coupling effect has been neglected, which is often the case for rolling bearings) formulae for k(x) is appreciably simplified. For y = 0, from equation (3.40), we get

(3.44)

Hence, for y = 0; A = 0. The stiffness expression (3.42) can be simplified to

(3.45)

with

(3.46)   (3.47)

Preloading is given as

(3.48)

where P_d is the diametral clearance (P_d = 2c_r). When x = 0, let k(x) = k(0) = k_o. From equation (3.45), we have

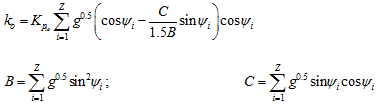(3.49)   (3.50)

We can have different level of preloading conditions as follows:

Case I:    g > 0 (Positive preloading). A simplified mathematical expression of the bearing stiffness is taken as

(3.51)

and

(3.52)

Let k(x=g) = k(g) = k_g. At x = 0, from equation (3.51), we get a= k_o; and at x = g, we get . So that the stiffness can be expressed as

(3.53)

Similarly, from equation (3.52) from information at x = g, we get

(3.54)

Case 2: g = 0 (No clearance). A simplified mathematical expression of the bearing stiffness is taken as

(3.55)

At x = c (c is a constant), we get b₂ = k_cc^-2 with k_c = k(c). So that the stiffness can be expressed as

(3.56)

Case3:  g < 0 (pre-clearance or negative preload). A simplified mathematical expression of the bearing stiffness is taken as

(3.57)

For x = d (, where d is a constant), we get b₃ = k_d(d)^-3/2 with k_d = k(d). So that the stiffness can be expressed as

(3.58)

Equations (3.53), (3.54), (3.56), and (3.58) are basically simplified expressions for the bearing stiffness expression given by equation (3.45). These forms of the bearing stiffness can be used to analyse the nonlinear behaviour of rotor bearing systems (Tiwari, 1995). It should be noted that the analysis presented here can be extended to roller bearings also by taking load-deflection exponent equals to n = 1.08. Various geometrical relations for roller bearings would be

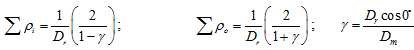(3.59)

and

(3.60)

where D_r is the nominal roller diameter.

Example 3.3: Obtain the stiffness of a ball bearing with the following specification: deep groove ball bearings, bearing no. 6200, d = bore diameter = 10 mm, D  = outer diameter = 30 mm and width = 9 mm.

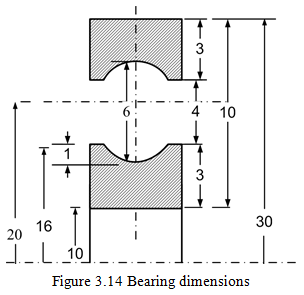
Solution: In general, the internal geometric dimensions of the bearings are not provided in the Bearing Manufacture’s Catalogs (e.g., SKF General Catalog). These dimensions can be either measured after disassembling the bearing or it can approximately be calculated by the expressions in terms of boundary dimensions of the bearing provided in the Bearing Catalogs. for obtaining the stiffness of the bearing. General proportions for ball bearings, as shown in Figure 3.14, are obtained as follows (PSG, 1982):

The pitch diameter or the mean diameter: = 20 mm.

The diameter of the ball D_b = 0.3(D - d) = 6 mm.

The radial thickness of rings, s =0.15(D - d) = 3 mm.

The number of ball,. Hence Z = 6 can be taken.

The inner and outer ring groove radius of curvatures, r_i = r_o = 0.515D = 3.09 mm.

For zero radial clearance, the inner and outer ring diameters at raceway grooves are:

d_o = 20 + 6 = 26 mm; d_i = 20 - 6 = 14 mm

For a ball bearing of the bore diameter 10 mm; from the design data books we have radial clearance is of the order of 2-13 μm. Let us for the present example take the maximum clearance, hence g = -13 X 10^-3 mm.