For a given load, the size of the contact area (i.e., the elastic deformation between the rolling element and the raceway) determines the magnitude of stresses in the bearing components. In case of a ball bearing the contact area between the rolling element and the raceway is zero when no load is applied. It is a case of the point contact. For two bodies with point contact (with a load the point contact would become an area contact with the contact area (of very small quantity) as an ellipse for the ball bearing), made of same material and subjected to a compressive load F, from the Hertzian contact theory, we have

(3.3)

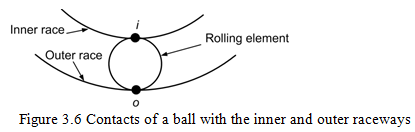
where the subscript p represents the point contact, δ_p is the contact deformation in a point contact, and K_p is a load-deformation constant for a single point contact, which depends upon material properties and the geometry of contacting surfaces (Changsen, 1991; Harris, 2001). . In case of rolling element bearings, the elastic deformation takes place at both the inner raceway and the outer raceway with the rolling element (Figure 3.6).

The total deformation, δ, at a single rolling element location is given by (noting the form of equation (3.3) for each of the contact points at the inner and outer raceways)

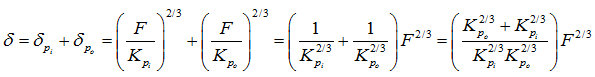(3.4)

where subscripts i and o represent the inner and outer raceways. Equation (3.4) can be rewritten as

(3.5)

with

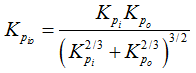(3.6)

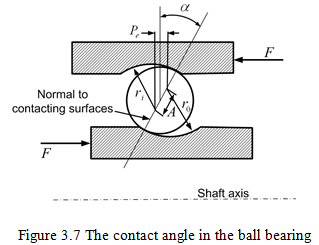
where is the load-deformation constant for two point contacts of a ball with raceways.  (units in N-mm^-3/2) depends mainly upon bearings curvature ratio ƒ as defined in equation (3.7) and other terms, i.e.D_bD_m (Fig. 3.3) and ; whereD_m is the pitch diameter of the bearing and α is the contact angle (refer Fig. 3.7). The curvature ratio is defined as

(3.7)

where r is the radius of curvature of the raceway in mm with subscripts i or o for the inner raceway or outer raceway, respectively.

 

For detailed accurate calculation of  readers are referred to subsequent section examples. If dependence of on the bearing size, D, and contact angle, , is neglected, then for (which is usually the case for deep groove ball bearings); then values of  may be obtained directly as (Palmgren, 1959)

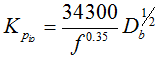(3.8)

For roller-bearings, the corresponding load-deformation constant (subscript l represents the line contact) depends only on the effective length of roller l_e and approximately it is given as

(3.9)

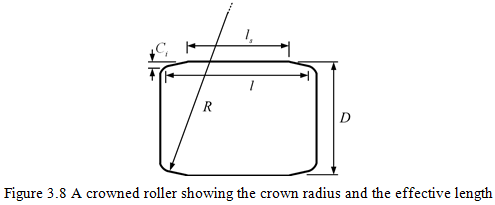
The effective length of rollers is that length of roller which is actually in contact with the raceway, usually this is equal to the actual roller length minus the roller corner radii as shown in Figure 3.8. The relationship between the load-deformation constant, the applied compressive load, and the elastic deformation at a single roller due to inner and outer raceway contacts is given by

(3.10)

with

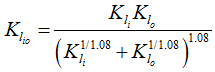(3.11)

 

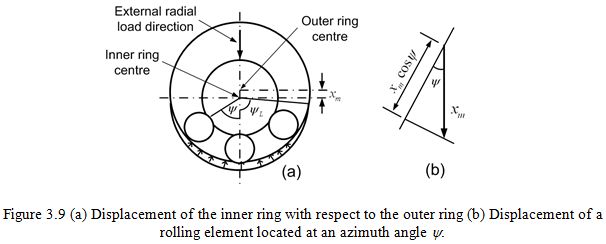
In roller bearings there is a line contact between the rolling element and bearing raceways at no load conditions. Equations (3.5) to (3.10) indicate relationships of elastic deformation at one rolling element under the action of a single compressive force applied at the rolling element (i.e., the ball or roller). In real bearings where more than one rolling element is in compression (i.e., all the rolling elements within the load zone), the effect at each element should be incorporated as shown in Figure 3.9.