Bearing identification number: Identification numbers of rolling bearings are composed of the basic numbers and the auxiliary codes. The basic numbers are made up of a bearing series symbol, and a dimension series symbol. For example, in bearing basic no. 6204, various numbers representation are as follows: 4 represents diameter series (other options: 8, 9, 0, 1, 2, 3 and 4); 0 represents width series (other options: 1, 2, 3, 4, 5, and 6) and 62 represents bearing series (62 for radial ball bearing, 72 for angular contact ball bearing, 320 for tapered roller bearing, etc.). The auxiliary codes are attached to basic number to identify seal or shield codes, race configuration code, clearance code and tolerance class codes (Harris, 2001).
In rolling element bearings, very high speeds are those speeds having DN number (is defined as d x N, where d is the bore diameter in mm and N is the bearing operating speed in rpm) more than 3 millions. For example, for d = 30 mm and N = 1,00,000 rpm or d = 100 mm and N = 30,000 rpm or d = 600 mm and N = 5,000 rpm would give the same DN number of 3 millions. High-speed bearings find applications in aerospace and space technologies. Applications of low speed bearings are (i) gyroscopes: they have very long life of the order of 15 years and they are very high precision bearings. Lubrication for such bearings is quite challenging since it requires about one to two drops per year. Micro and nano-pumps may have very useful applications for such lubrication flow rate; (ii) rotary kiln: it is used in cement factories and have rotational speed of 2 to 3 rpm, however, the size of bore diameter is of the order of 4 m or so.

Frictional Torque and Power: The rolling bearing frictional torque, Mt, can be obtained as
| (3.1) |
where f is the coefficient of friction (a general average of about 0.001, see Table 3.2), d is the bore diameter of the bearing in m and F is the radial or axial load as specified in N. The frictional power loss, P, is given as
| (3.2) |
where N is the shaft angular speed in rev/min. The heat generation and temperature distribution at rolling contact is very important since diametral clearance of rolling bearing changes with temperatures. A more detailed treatment can be found in Kashyap & Tiwari (2006) and Harris (2001).
Estimation of elastic parameters of bearings involves establishing a relationship between the incident load on the bearing, and its resultant deformation. The classical solution for the local stress and deformation of two elastic bodies apparently contacting at a single point was established by Hertz in (1896). Hertz's analysis is applied to surface stresses caused by a concentrated force, applied perpendicular to the surface. In the determination of contact deformation versus load, the concentrated load applied normal to the surface alone is considered (i.e., by neglecting the friction forces), for most rolling element bearing applications.
It is possible to determine how the applied load on the bearing is distributed among the balls or rollers (or rolling elements) by considering equilibrium of rolling elements and the bearing. To do this, it is necessary to develop load-deflection relationships for rolling elements contacting raceways. Most rolling bearing applications involve steady-state rotation of either the inner or outer raceways or both. Rolling element centrifugal forces, gyroscopic moments, and the frictional forces and moments do not significantly influence this load distribution in most general purpose applications. Theoretical models (Palmgren, 1959; Ragulskis et al., 1974; Harris, 1984; Eschamann et al. 1985; Stolarski, 1990) are available for estimation of bearing stiffness under static loading conditions. In the next section these analysis will be treated in the most simplistic way.
3.1.1 Linear radial stiffness of rolling bearings
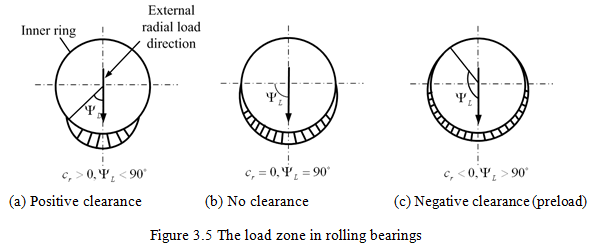
The amount by which a shaft, supported by bearing, can be displaced from its concentric position by a given load is of our interest. This displacement depends upon the elastic deformation of the bearing raceways and of rolling elements themselves. The elastic deformation of these components depends upon the geometry and the material of the bearing, and on the bearing internal clearance or preload (i.e. the negative clearance). The bearing internal clearance is an important factor because it determines the size of the stressed area of the rings (i.e. the load zone angle, YL) as shown in Figure 3.5. Lesser the clearance (or more the preload), then more and more rolling elements will share the external applied load from the shaft. This results in lesser load per rolling element and hence lesser maximum contact stress. However, preload may reduce the life of bearings due to high fatigue stresses in rolling elements, especially in high temperature environments.