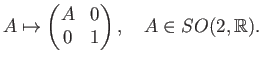- Show that the sphere
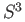 is isomorphic (as a topological group) to
is isomorphic (as a topological group) to
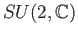 .
.
- Show that the center of the group of non-zero quaternions is the set of non-zero real numbers.
In the light of this explain why ker
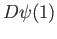 in lemma (22.6) is non-trivial.
in lemma (22.6) is non-trivial.
- Explain why the map
 defined in theorem (22.8) is bijective.
defined in theorem (22.8) is bijective.
- Verify the properties of the map
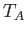 in the proof of theorem (22.10). Also fill in the details
concerning the properties of the map
in the proof of theorem (22.10). Also fill in the details
concerning the properties of the map  (except for the claims made concerning its derivative).
(except for the claims made concerning its derivative).
- Use exercise 4 to find a generator of
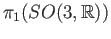 . Let
. Let
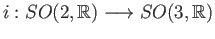 be given by
be given by
Show that
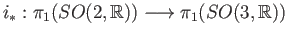 is surjective.
is surjective.
in
Lectures - XXIII and XXIV Coproducts and Pushouts
in
We now discuss further categorical constructions that are essential for the
formulation of the Seifert Van Kampen theorem.
We first discuss the notion of coproducts which is
a prerequisite for a proof of the existence of push-outs.
The coproduct is popularly known as the free product in the context of
groups but we shall also use the term coproduct
which seems more appropriate from a
categorical point of view ([11], p. 71). The notion of coproducts has
already been introduced in the exercises to lecture 7 for the categories Top and AbGr where it is popularly known as the disjoint
union and the direct sum respectively. However the
construction is more complicated in the category Gr.
The coproduct is defined in terms of a universal property.
Subsections
nisha
2012-03-20