Given two groups 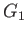 and
and 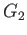 , their coproduct is a group
, their coproduct is a group  together with a pair of group homomorphisms
together with a pair of group homomorphisms
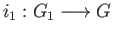 and
and
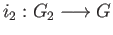 such that given any group
such that given any group  and group homomorphisms
and group homomorphisms
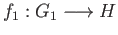 and
and
 there exists a unique homomorphism
there exists a unique homomorphism
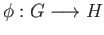 such that
such that
summarized in the following diagram (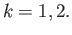 ):
):
The definition immediately generalizes to any arbitrary (not necessarily finite) collection of groups.
The uniqueness clause in the definition is important and the following theorem hinges upon it.
nisha
2012-03-20
![$\displaystyle \xymatrix{
G_k \ar[rr]^{i_k}\ar[rd]_{f_k} & & G \ar[ld]^{\phi}\\
& H
}
$](img1742.png)