Denoting by 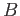 the set of generators
the set of generators
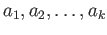 of
of 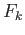 , any collection
, any collection 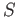 of words
of words
gives rise to a group
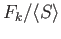 where
where
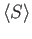 denotes the normal subgroup generated by
denotes the normal subgroup generated by 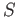 .
Conversely, let
.
Conversely, let  be a finitely generated group and
be a finitely generated group and  be as in the theorem.
We take a set
be as in the theorem.
We take a set 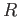 of words (23.2) generating the kernel of
of words (23.2) generating the kernel of  and write
and write
The elements of 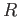 are called relators and
the set of equations
are called relators and
the set of equations
obtained by setting each relator to 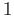 are called the relations for the group with respect to
are called the relations for the group with respect to  .
The list of generators
.
The list of generators
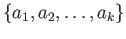 and relations
among them uniquely specifies
and relations
among them uniquely specifies  through equation (23.3). If a relation in the list (23.4) is
a consequence of others, for example if one of them is the product of two others, we may clearly drop it from the list
thereby shortening the list.
In practice one would try to keep the list of relations down to a minimum. Such a description of
through equation (23.3). If a relation in the list (23.4) is
a consequence of others, for example if one of them is the product of two others, we may clearly drop it from the list
thereby shortening the list.
In practice one would try to keep the list of relations down to a minimum. Such a description of  is called a
presentation of the group
is called a
presentation of the group  through generators and relations. A group in general has many presentations and
it is usually very difficult to decide whether or not two presentations represent the same group.
nisha
2012-03-20
through generators and relations. A group in general has many presentations and
it is usually very difficult to decide whether or not two presentations represent the same group.
nisha
2012-03-20