Let  be generated by
be generated by
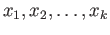 and for each
and for each
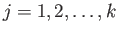 let
let 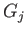 be the infinite cyclic group with generator
be the infinite cyclic group with generator 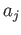 , regarded as a subgroup of
, regarded as a subgroup of 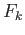 .
Applying the definition of the coproduct to the collection of
group homomorphisms
.
Applying the definition of the coproduct to the collection of
group homomorphisms
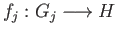 defined by
defined by
we get a group homomorphism
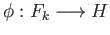 such that
such that
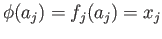 . It is clear that
. It is clear that
 is surjective and the proof is complete.
is surjective and the proof is complete.
nisha
2012-03-20