Let us begin with Gr and a given pair of morphisms
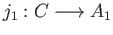 and
and
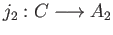 . Let
. Let  be the coproduct of the groups
be the coproduct of the groups 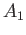 and
and 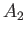 . We regard
. We regard 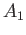 and
and 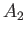 as
subgroups of
as
subgroups of  . Let
. Let 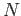 be the normal subgroup of
be the normal subgroup of  generated by
generated by
and
 be the quotient map.
We claim that
be the quotient map.
We claim that 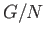 qualifies as the push-out with the associated homomorphisms
qualifies as the push-out with the associated homomorphisms
where 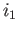 and
and 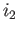 are the inclusions of
are the inclusions of 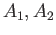 in
in  .
Since
.
Since
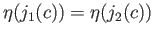 ,
we see that
,
we see that
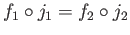 . To check the universal property, let
. To check the universal property, let
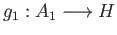 and
and
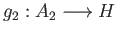 be a pair of morphisms such that
be a pair of morphisms such that
Aside from (23.10), by definition of coproduct, there exists a unique homomorphism
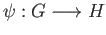 such that
such that
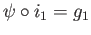 and
and
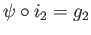 from which follows easily
that the kernel of
from which follows easily
that the kernel of 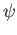 contains
contains 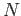 . Let
. Let
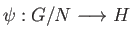 be the unique map such that
be the unique map such that
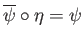 .
Then
.
Then
which means
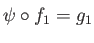 and
and
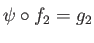 .
That completes the job of verifying that
.
That completes the job of verifying that 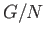 is indeed the push-out.
Note that we have only used the definition of coproducts and the most basic property of quotients. As a result the proof goes through verbatim
for the other two situations as we shall see.
Leaving aside the case of abelian groups we pass
on to the category Top.
is indeed the push-out.
Note that we have only used the definition of coproducts and the most basic property of quotients. As a result the proof goes through verbatim
for the other two situations as we shall see.
Leaving aside the case of abelian groups we pass
on to the category Top.
Well, changing notations to suit the need, let
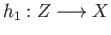 and
and
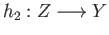 be a pair of continuous functions
and
be a pair of continuous functions
and 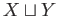 be the disjoint
union of
be the disjoint
union of  and
and  , and
, and
 ,
,
 be the canonical inclusions.
For each
be the canonical inclusions.
For each 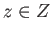 we identify the points
we identify the points
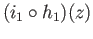 and
and
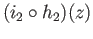 in
in 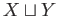 and
and 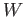 be the quotient space with the projection map
be the quotient space with the projection map
We claim that 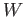 qualifies to be the push-out with associated morphisms
qualifies to be the push-out with associated morphisms
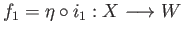 and
and
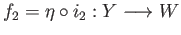 . To check the first condition observe that since
. To check the first condition observe that since
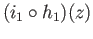 and
and
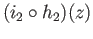 are identified,
are identified,
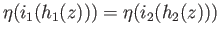 which means
which means
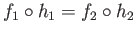 .
Turning now to the universal property let
.
Turning now to the universal property let
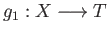 and
and
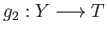 be two continuous maps such that
be two continuous maps such that
Aside from (23.11), since 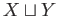 is the coproduct in Top,
there is a unique continuous map
is the coproduct in Top,
there is a unique continuous map
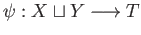 such that
such that
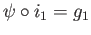 and
and
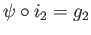 . Now (23.11) implies that
. Now (23.11) implies that 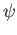 respects the identification and so there is a unique
respects the identification and so there is a unique
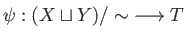 such that
such that
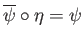 . By the universal property of the quotient,
. By the universal property of the quotient,
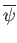 is continuous and
is continuous and
and likewise
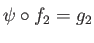 . That suffices for a proof.
nisha
2012-03-20
. That suffices for a proof.
nisha
2012-03-20
![]() and
and
![]() be a pair of continuous functions
and
be a pair of continuous functions
and ![]() be the disjoint
union of
be the disjoint
union of ![]() and
and ![]() , and
, and
![]() ,
,
![]() be the canonical inclusions.
For each
be the canonical inclusions.
For each ![]() we identify the points
we identify the points
![]() and
and
![]() in
in ![]() and
and ![]() be the quotient space with the projection map
be the quotient space with the projection map