- Show that the maps
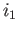 and
and 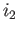 in definition (23.1) are injective and that
the images of
in definition (23.1) are injective and that
the images of 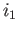 and
and 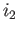 generate
generate 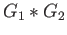 .
Hint: Use the universal property with
.
Hint: Use the universal property with
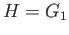 ,
, 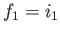 and
and 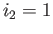 .
.
- Show that abelianizing a free group on
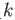 generators results in a group isomorphic to the direct sum of
generators results in a group isomorphic to the direct sum of 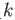 copies of
copies of
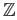 . Use the fact that the coproduct in AbGr is the direct sum.
. Use the fact that the coproduct in AbGr is the direct sum.
- Is there a surjective group homomorphism from the direct sum
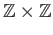 onto
onto
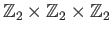 ?
Prove that if
?
Prove that if 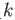 and
and 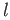 are distinct positive integers,
the free group on
are distinct positive integers,
the free group on 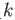 generators is not isomorphic to the free group on
generators is not isomorphic to the free group on 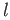 generators.
generators.
- Show that
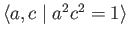 is also a presentation of the fundamental group of the Klein's bottle.
is also a presentation of the fundamental group of the Klein's bottle.
- Construct the push-out for the pair
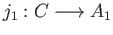 and
and
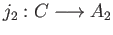 in the category AbGr?
in the category AbGr?
- Suppose that
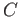 is the trivial group in the definition of push-out in the category Gr, show that the resulting group is the coproduct of the
two given groups. What happens in the category AbGr?
Describe explicitly the construction of the group specifying the subgroup
that is being factored out.
is the trivial group in the definition of push-out in the category Gr, show that the resulting group is the coproduct of the
two given groups. What happens in the category AbGr?
Describe explicitly the construction of the group specifying the subgroup
that is being factored out.
in
Lecture - XXV Adjunction Spaces
in
The notion of push-outs in the category Top leads to an important class of spaces known as adjunction spaces.
We shall see that most of the important spaces encountered are adjunction spaces.
This lecture may be regarded as one on important examples of topological spaces.
Subsections
nisha
2012-03-20