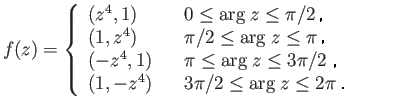We now show that the Klein's bottle and the torus are obtained by
attaching a two cell to the figure eight space
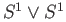 . In both cases we take
. In both cases we take 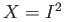 to be the two cell,
to be the two cell,
 the boundary of
the boundary of 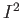 and
and
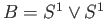 regarded as a subset of
regarded as a subset of
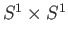 namely
namely
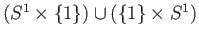 .
The distinguishing factor is that
the attaching map
.
The distinguishing factor is that
the attaching map
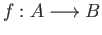 is different in the two cases.
is different in the two cases.
- For the torus we define
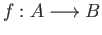 to be the continuous surjection
to be the continuous surjection
It is geometrically clear that
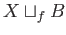 is a torus but we demonstrate this formally owing to the importance of the
type of argument involved. Let
is a torus but we demonstrate this formally owing to the importance of the
type of argument involved. Let
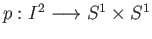 be the quotient map,
be the quotient map,
 the inclusion map and
the inclusion map and
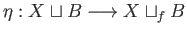 the quotient map. The map
the quotient map. The map
given by
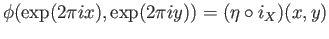 is well-defined, bijective and
its continuity follows from the fact that
is well-defined, bijective and
its continuity follows from the fact that
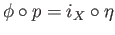 and
and
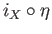 is continuous. Finally the compactness of
is continuous. Finally the compactness of
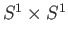 and the fact that
and the fact that
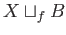 is Hausdorff shows that
is Hausdorff shows that  is a homeomorphism.
is a homeomorphism.
- The argument for the Klein's bottle proceeds along similar lines and we merely indicate the attaching map
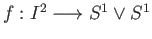 namely,
namely,
- It is sometimes convenient to take the closed unit disc
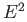 as the two cell. But the attaching map
as the two cell. But the attaching map
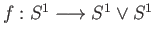 would be slightly more complicated to write down. For the Klein's bottle the
attaching map is given by
would be slightly more complicated to write down. For the Klein's bottle the
attaching map is given by
For the torus the attaching map is obtained from (25.5) by suppressing the negative signs in the last two expressions.
The student is invited to work out a similar construction for the double torus as well.
nisha
2012-03-20