The proof writes itself out. Suppose that
![$ G:X\times [0,1]\longrightarrow Y$](img1971.png) is a homotopy between
is a homotopy between  and the
constant map taking the value
and the
constant map taking the value 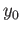 say,
say,
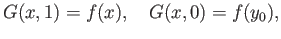
for all
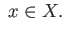
The second equation in (25.12) says that  respects the identification made on
respects the identification made on
![$ X\times [0,1]$](img1974.png) to yield
to yield
![$ (X\times [0,1])/(X\times\{0\})$](img1975.png) whereby we conclude the existence of a map
whereby we conclude the existence of a map
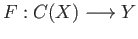 satisfying
satisfying
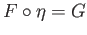 . This map
. This map 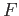 is continuous by the universal property
and the first equation in (25.12) gives
is continuous by the universal property
and the first equation in (25.12) gives
![$ F[x, 1] = G(x, 1) = f(x)$](img1977.png) . The proof of necessity is complete.
. The proof of necessity is complete.
Conversely suppose given a continuous map
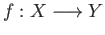 such that there is a
such that there is a
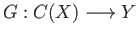 with
with
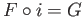 . Denoting by
. Denoting by 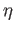 the quotient map
the quotient map
![$ X\times [0,1]\longrightarrow C(X)$](img1980.png) , the map
, the map
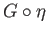 provides a homotopy
between
provides a homotopy
between  the constant map.
the constant map. 
nisha
2012-03-20
![]() such that there is a
such that there is a
![]() with
with
![]() . Denoting by
. Denoting by ![]() the quotient map
the quotient map
![]() , the map
, the map
![]() provides a homotopy
between
provides a homotopy
between ![]() the constant map.
the constant map. ![]()