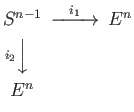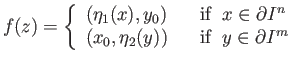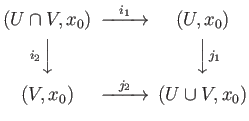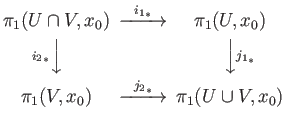- We have obtained
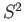 by attaching
by attaching 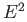 to a singleton with the
attaching map as the constant map on the boundary of
to a singleton with the
attaching map as the constant map on the boundary of 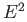 .
Discuss how would you obtain
.
Discuss how would you obtain  analogously as an adjunction space.
analogously as an adjunction space.
- Show that if
 and
and 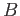 are connected/path-connected then
are connected/path-connected then
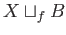 is connected/path-connected.
is connected/path-connected.
- Describe the push out resulting from the diagram
- Show that
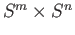 results from attaching an
results from attaching an 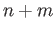 cell to
cell to
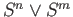 . Hint: Let
. Hint: Let 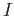 denote
denote ![$ [0, 1]$](img13.png) and
define a map
and
define a map
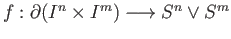 as follows
as follows
and
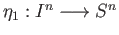 and
and
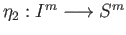 are the quotient maps of exercise 1.
are the quotient maps of exercise 1.
- Prove theorem (25.3).
- Fill in the details in examples (25.4) and (25.5).
in
Lecture - XXVI Seifert Van Kampen theorem and knots
in
This is one of the most famous theorem concerning the fundamental group which serves
as a tool for computations and applications to combinatorial group theory.
If  and
and  are path connected open
subsets of a topological space such that
are path connected open
subsets of a topological space such that 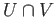 is path connected,
the theorem provides information on the geometry of
is path connected,
the theorem provides information on the geometry of
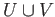 in terms of the geometry of
in terms of the geometry of  ,
,  and
and 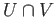 .
In precise terms it states that the
.
In precise terms it states that the 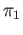 functor maps the push-out diagram of pointed topological spaces with
functor maps the push-out diagram of pointed topological spaces with
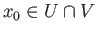 ,
to the push-out diagram of groups:
thereby giving a precise description of the group
,
to the push-out diagram of groups:
thereby giving a precise description of the group
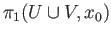 in terms of the groups
in terms of the groups
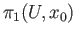 ,
,
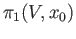 and
and
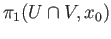 . Thus
. Thus
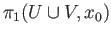 is the
free product of
is the
free product of
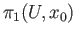 and
and
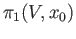 amalgamated along
amalgamated along
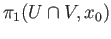 .
The theorem enables us to calculate quickly the fundamental
groups of several important spaces.
.
The theorem enables us to calculate quickly the fundamental
groups of several important spaces.
Subsections
nisha
2012-03-20