Let 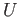 ,
, 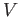 be open path connected subsets of a topological
space such that
be open path connected subsets of a topological
space such that 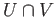 is path connected. Let
is path connected. Let
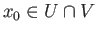 and
and
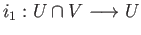 ,
,
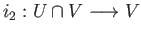 denote the inclusion maps. Then
denote the inclusion maps. Then
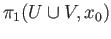 is the free product (coproduct)
of
is the free product (coproduct)
of
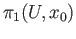 and
and
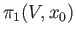 amalgamated along
amalgamated along
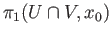 with respect to the maps
with respect to the maps
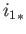 and
and 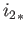 . That is to say if
. That is to say if 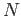 is the normal subgroup
is the normal subgroup
then the fundamental group of 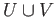 is given by
is given by
Considering
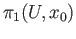 and
and
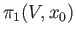 as subgroups of
as subgroups of
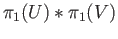 , their images in the quotient group
generate
, their images in the quotient group
generate
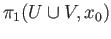 .
.
The result may be elegantly stated using a push-out diagram namely,
nisha
2012-03-20