Theorem 26.2 (Seifert and Van Kampen - version II):

Let $U$, $V$ be open path connected subsets of a topological space such that $U\cap V$ is path connected. Let $x_0\in U\cap V$ and $i_1:U\cap V\longrightarrow U$, $i_2:U\cap V\longrightarrow V$ denote the inclusion maps. Then the push-out data

$\begin{CD} \pi_1(U\cap V, x_0) @> {i_1}_* >> \pi_1(U, x_0) \\ @V{{i_2}_*}VV @.\\ \pi_1(V, x_0) @. \\ \end{CD}$

may be completed to yield the push-out square

$\begin{CD} \pi_1(U\cap V, x_0) @> {i_1}_* >> \pi_1(U, x_0) \\ @V{{i_2}_*}VV @VV{{j_1}_*}V\\ \pi_1(V, x_0) @> {j_2}_* >> \pi_1(U\cup V, x_0) \\ \end{CD}$

where the maps $j_1:U\longrightarrow U\cup V$ and $j_2:V\longrightarrow U\cup V$ are inclusions.

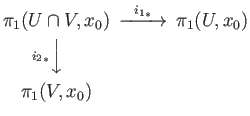
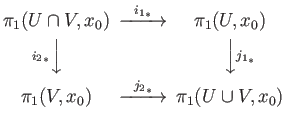
The proof is neatly presented on pages 110-113 of the book by J. Vick and need not be repeated here. Instead we move on to its applications to the computation of the fundamental groups of certain spaces.