Suppose that  ,
,  are open path-connected subsets of a topological space such that
are open path-connected subsets of a topological space such that
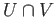 and
and  are simply connected then with a base point
are simply connected then with a base point
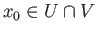 ,
,
We turn to an important example to illustrate the use of this corollary. Regard
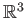 as a subset of
as a subset of 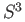 via the
stereo-graphic projection and
via the
stereo-graphic projection and  be a compact subset of
be a compact subset of
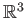 such that the complement
such that the complement
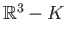 is connected. We then have the following result.
is connected. We then have the following result.
nisha
2012-03-20