Let us consider the space
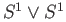 given by the union of two circles
of radius one in the plane touching each other externally at the origin.
We take
given by the union of two circles
of radius one in the plane touching each other externally at the origin.
We take  and
and  to be the open sets
obtained by deleting one of the points of each lobe (not the common point!). Then the circle is a deformation retract of
both
to be the open sets
obtained by deleting one of the points of each lobe (not the common point!). Then the circle is a deformation retract of
both  and
and  and
and 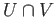 deformation retracts to the origin. Thus
deformation retracts to the origin. Thus
The last clause in theorem (26.1) also provides the generators of the fundamental group. Assuming the circles
to centered at 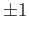 , the generators are given by the homotopy classes of the loops
, the generators are given by the homotopy classes of the loops
The generalization to a wedge of  circles is left as an exercise.
circles is left as an exercise.
nisha
2012-03-20