Proof:

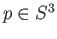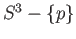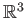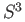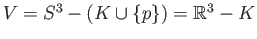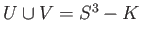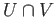Let $p \in S^3$ denote the north-pole using which we project $S^3 - \{p\}$ stereo-graphically onto $\mathbb{R}^3$. Since $K$ is compact there is a neighborhood $U$ of $p$ in $S^3$ homeomorphic to a ball which does not intersect $K$. Taking $V = S^3 - (K\cup\{p\}) = \mathbb{R}^3 - K$, we see that $U\cup V = S^3 - K$ and $U\cap V$ deformation retracts to 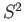$S^2$. The result now follows from the previous theorem.