We proceed along the same lines using the convenient form (25.5).
Denoting by  either the torus or the Klein's bottle and
either the torus or the Klein's bottle and  to be the origin, we see that
to be the origin, we see that 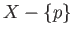 deformation retracts to the figure eight loop and, in analogy with (26.6),
the generators for the free group
deformation retracts to the figure eight loop and, in analogy with (26.6),
the generators for the free group
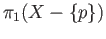 are given by
are given by
We take  to be the open unit disc,
to be the open unit disc,  to be
to be 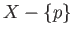 and the class of (26.5) as the generator for
and the class of (26.5) as the generator for
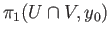 where the base point
where the base point 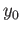 is
is 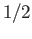 .
Taking an auxiliary path
.
Taking an auxiliary path 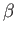 joining
joining
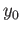 and the point
and the point  common to both
common to both
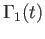 and
and
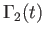 , we get the generators
, we get the generators
![$\displaystyle [\beta *\Gamma_1 *\beta^{-1}]\phantom{X}$](img2052.png)
and
![$\displaystyle \phantom{X}[\beta *\Gamma_2 *\beta^{-1}] \eqno(26.9)
$](img2053.png)
for
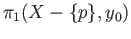 .
The deformation of the previous example (exercise (1)) can be employed here again and this time we get
.
The deformation of the previous example (exercise (1)) can be employed here again and this time we get
for the torus whereas for the Klein's bottle we get instead
One could also work with the other models described in example (25.3) where the spaces are obtained
by identifying the opposite edges of a square. The homotopy
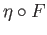 of the last example
would have to be modified to
of the last example
would have to be modified to
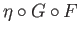 where
where  is a certain
homeomorphism from the unit
disc onto the square
is a certain
homeomorphism from the unit
disc onto the square
![$ [0, 1]\times [0, 1]$](img213.png) .
.
Denoting the generators (26.9) of
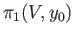 by
by 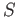 and
and 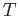 we are ready to apply corollary (26.7) since
(26.10) gives us the image of the map
we are ready to apply corollary (26.7) since
(26.10) gives us the image of the map 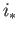 . The
fundamental group of the torus is then
. The
fundamental group of the torus is then
and the fundamental group of the Klein's bottle is
nisha
2012-03-20
![]() by
by ![]() and
and ![]() we are ready to apply corollary (26.7) since
(26.10) gives us the image of the map
we are ready to apply corollary (26.7) since
(26.10) gives us the image of the map ![]() . The
fundamental group of the torus is then
. The
fundamental group of the torus is then