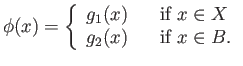We first define the associated maps
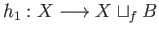 and
and
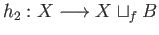 . Let
. Let
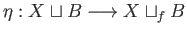 be the quotient map and
be the quotient map and
 and
and
 denote the inclusions.
Then the associated maps
denote the inclusions.
Then the associated maps 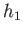 and
and 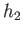 given by
given by
For any 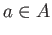 we have
we have
Recalling the identifications we see that
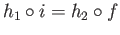 .
We now check the universal property. Suppose
.
We now check the universal property. Suppose 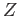 is a topological space and
is a topological space and
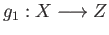 ,
,
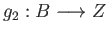 are continuous maps such that
are continuous maps such that
Define the continuous map
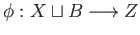 as
as
Condition (25.2) now shows that there is a unique map
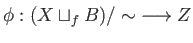 such that
such that
The universal property of the quotient implies that
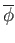 is continuous.
Equations (25.1)-(25.3) immediately give
is continuous.
Equations (25.1)-(25.3) immediately give
thereby completing the verification of the universal property.
nisha
2012-03-20