If
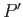 with morphisms
with morphisms
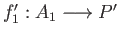 and
and
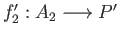 is another candidate we may apply the
universal property to get a map
is another candidate we may apply the
universal property to get a map
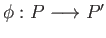 such that
such that
Reciprocally since
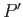 is a push out, there is a map
is a push out, there is a map
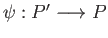 such that
such that
Combining we see that
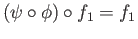 and
and
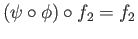 .
We see that both
.
We see that both
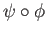 and
id
and
id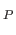 satisfy the universal property with
satisfy the universal property with  ,
, 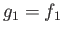 and
and 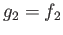 . The uniqueness clause
in the definition gives
. The uniqueness clause
in the definition gives
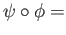 id
id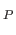 .
Likewise we get
.
Likewise we get
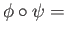 id
id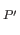 and the proof is complete.
and the proof is complete.
nisha
2012-03-20