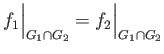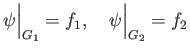Let us now work in the category Top and recast the gluing lemma in terms of the push-out construction.
Take a pair of open sets 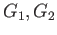 in a topological space
in a topological space  and the inclusions
and the inclusions
The push out for this pair is the space
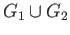 together with inclusion maps
together with inclusion maps
To see this suppose that  is a topological space and
is a topological space and
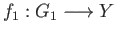 and
and
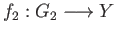 are a pair of continuous
maps such that
are a pair of continuous
maps such that
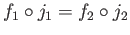 then
then
The gluing lemma now says that there exists a unique map
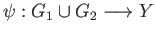 such that
such that
which means
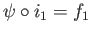 and
and
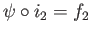 as desired.
Instead of a pair of open subsets of a topological space one could choose a pair of closed sets.
as desired.
Instead of a pair of open subsets of a topological space one could choose a pair of closed sets.
nisha
2012-03-20