To establish uniqueness, suppose that
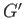 is another candidate for the coproduct with the associated homomorphisms
is another candidate for the coproduct with the associated homomorphisms
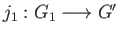 and
and
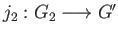 satisfying the universal property. Taking
satisfying the universal property. Taking 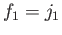 and
and
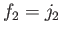 in the definition, there exists a homomorphism
in the definition, there exists a homomorphism
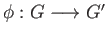 such that
such that
But since
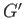 is also a coproduct we obtain reciprocally a group homomorphism
is also a coproduct we obtain reciprocally a group homomorphism
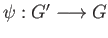 such that
such that
Combining the two we get
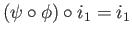 and
and
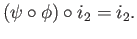 We see that the identity map id
We see that the identity map id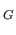 as well as
as well as
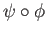 satisfy the universal property with
satisfy the universal property with 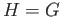 ,
, 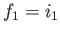 and
and 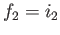 .
The uniqueness clause in the definition of the coproduct gives
.
The uniqueness clause in the definition of the coproduct gives
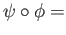 id
id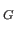 Interchanging the roles of
Interchanging the roles of  and
and
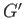 we get
we get
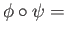 id
id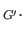 We leave it to the student to show that the maps
We leave it to the student to show that the maps 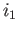 and
and 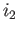 are injective.
are injective.
nisha
2012-03-20